题目内容
已知数列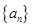 满足
满足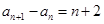 (
(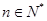 )且
)且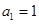
(1)求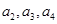 的值
的值
(2)求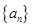 的通项公式
的通项公式
(3)令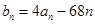 ,求
,求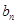 的最小值及此时
的最小值及此时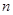 的值
的值
【答案】
(1) (2)
(2) (3)
(3)
【解析】
试题分析:(1)因为 ,且
,且
所以
(2)因为 ,所以
,所以 ,
,
这n-1个式子相加可得
(3)由(1)知

因为 ,结合二次函数的性质可以得到
,结合二次函数的性质可以得到
考点:本小题主要考查累加法求数列的通项公式和数列的函数性质的应用.
点评:数列是一类特殊的函数,所以有时利用函数的性质解决数列问题,不过要注意

练习册系列答案
相关题目
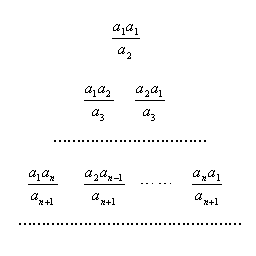
 满足
满足 ,
, ,且对任意
,且对任意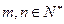 都有
都有
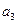 ,
, ;
;
 ,证明:
,证明: 是等差数列;
是等差数列;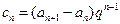
 ,求数列
,求数列 的前n项和
的前n项和 .
. 满足
满足 ,
, ,且
,且 ,
, 。
。 的前
的前 项和
项和 .
. 满足
满足 ,
, ,且
,且
 ;
;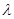 ,使得数列
,使得数列 为等差数列,求
为等差数列,求 满足
满足 ,
, (
( 且
且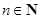 )
) 是常数列;
是常数列; 时,求数列
时,求数列 项和.
项和.