题目内容
已知数列 满足
满足 ,
, (
( 且
且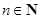 )
)
(Ⅰ)证明数列 是常数列;
是常数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)当 时,求数列
时,求数列 的前
的前 项和.
项和.
【答案】
(Ⅰ)证明:




即

 数列
数列 是常数列. …………………………………4分
是常数列. …………………………………4分
(Ⅱ)解:



 ……………………………6分
……………………………6分
当 时,
时, 是等比数列,首项
是等比数列,首项
 ,公比
,公比


当 时,
时, 满足上式. ………………………………8分
满足上式. ………………………………8分
(Ⅲ)解:





 ………………………………12分
………………………………12分
【解析】略

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
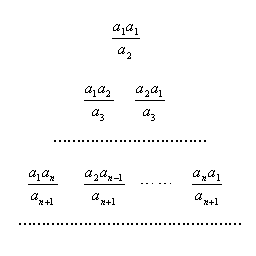
 满足
满足 ,
, ,且对任意
,且对任意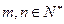 都有
都有
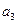 ,
, ;
;
 ,证明:
,证明: 是等差数列;
是等差数列;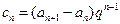
 ,求数列
,求数列 的前n项和
的前n项和 .
. 满足
满足 ,
, ,且
,且 ,
, 。
。 的前
的前 项和
项和 .
. 满足
满足 ,
, ,且
,且
 ;
;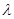 ,使得数列
,使得数列 为等差数列,求
为等差数列,求