题目内容
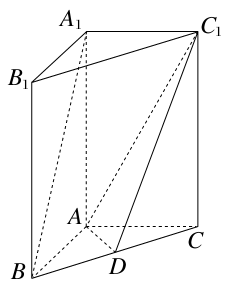
在长方体ABCD—A1B1C1D1中,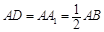 ,点E是棱AB上一点.且
,点E是棱AB上一点.且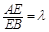 .
.
(1)证明: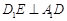 ;
;
(2)若二面角D1—EC—D的大小为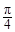 ,求
,求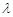 的值.
的值.
(1)详见解析;(2)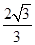 -1.
-1.
解析试题分析:(1)根据题意显然以D为原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系.此时不妨设AD =AA1=1,AB=2,则本表示出图中各点坐标,这里主要是要运用向量的知识表示出点E的坐标,这样就可表示出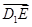 和
和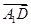 的坐标,利用向量垂直的充要条件:它们的数量积等于0,问题即可得证;(2)运用求平面法向量的知识分别求出:平面DEC的法向量为n1=(0,0,1);平面D1CE的法向量为
的坐标,利用向量垂直的充要条件:它们的数量积等于0,问题即可得证;(2)运用求平面法向量的知识分别求出:平面DEC的法向量为n1=(0,0,1);平面D1CE的法向量为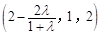 ,利用向量夹角知识可得:
,利用向量夹角知识可得: 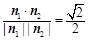 ,可解得
,可解得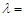 ±
±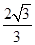 -1.利用E是棱AB上的一点,所以λ>0,故所求的λ值为
-1.利用E是棱AB上的一点,所以λ>0,故所求的λ值为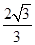 -1.
-1.
试题解析:(1)以D为原点,DA为x轴,DC为y轴,
DD1为z轴建立空间直角坐标系.
不妨设AD =AA1=1,AB=2,
则D(0,0,0),A(1,0,0),B(1,2,0),
C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1).
因为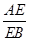 =λ,所以
=λ,所以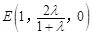 ,于是
,于是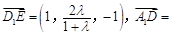 (-1,0,-1).
(-1,0,-1).
所以 .
.
故D1E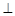 A1D. 5分
A1D. 5分
(2)因为D1D⊥平面ABCD,所以平面DEC的法向量为n1=(0,0,1).
又 ,
,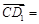 (0,-2,1).
(0,-2,1).
设平面D1CE的法向量为n2=(x,y,z),
则n2·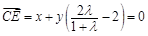 ,n2·
,n2· ,
,
所以向量n2的一个解为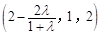 .
.
因为二面角D1—EC—D的大小为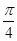 ,则
,则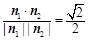 .
.
解得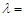 ±
±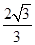 -1.
-1.
又因E是棱AB上的一点,所以λ>0,故所求的λ值为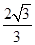 -1. 10分
-1. 10分
考点:1.向量的数量积的应用;2.平面的法向量;3.空位位置关系

 阅读快车系列答案
阅读快车系列答案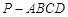 中,
中,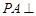 平面
平面 ,
,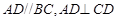 ,且
,且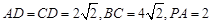 ,点
,点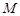 在
在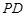 上.
上.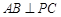 ;
;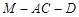 的大小为
的大小为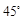 ,求
,求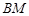 与平面
与平面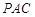 所成角的正弦值.
所成角的正弦值.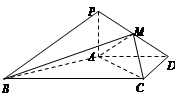
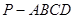 中,底面
中,底面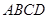 为矩形,
为矩形,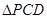 为等边三角形,
为等边三角形,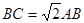 ,点
,点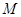 为
为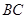 中点,平面
中点,平面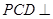 平面
平面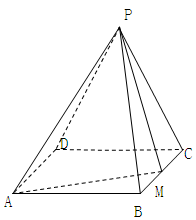
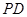 和
和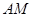 所成角的余弦值;
所成角的余弦值;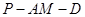 的大小.
的大小.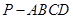 的底面的菱形,
的底面的菱形,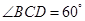 ,点
,点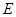 是
是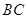 边的中点,
边的中点,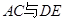 交于点
交于点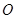 ,
,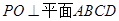
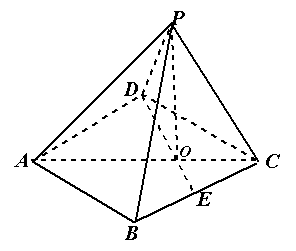
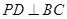 ;
; 的大小;
的大小;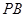 与
与 所成角的余弦值。
所成角的余弦值。 AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.
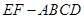 中,
中,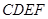 为边长为
为边长为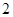 的正方形,
的正方形,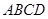 为直角梯形,
为直角梯形,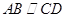 ,
,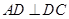 ,
,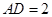 ,
,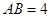 ,
,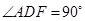 .
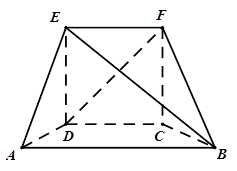
.
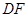 和
和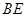 所成角的大小;
所成角的大小;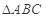 中,
中,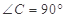 ,
, D、E分别是
D、E分别是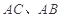 上的点,且
上的点,且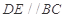 ,将
,将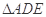 沿
沿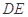 折起到
折起到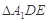 的位置,使
的位置,使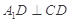 ,如图2.
,如图2.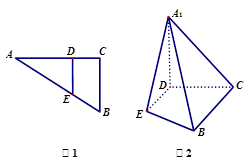
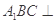 平面
平面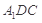 ;
;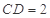 ,求
,求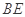 与平面
与平面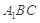 所成角的余弦值;
所成角的余弦值;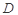 点在何处时,
点在何处时,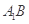 的长度最小,并求出最小值.
的长度最小,并求出最小值.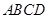 中,
中,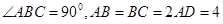 ,点
,点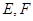 分别是
分别是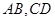 的中点,点
的中点,点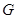 在
在 上,沿
上,沿
 平面
平面 .
.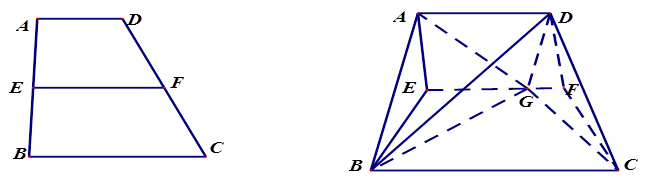
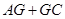 最小时,求证:
最小时,求证: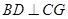 ;
;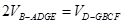 时,求二面角
时,求二面角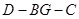 平面角的余弦值.
平面角的余弦值.