题目内容
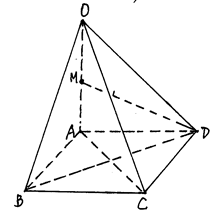
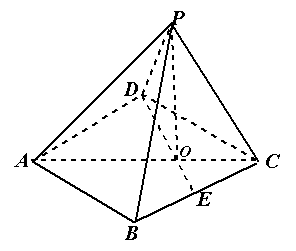
如图,已知四棱锥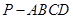 的底面的菱形,
的底面的菱形,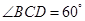 ,点
,点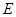 是
是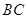 边的中点,
边的中点,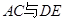 交于点
交于点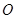 ,
,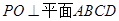
(1)求证: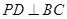 ;
;
(2)若 的大小;
的大小;
(3)在(2)的条件下,求异面直线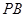 与
与 所成角的余弦值。
所成角的余弦值。
(1)(2) (3)
(3)
解析试题分析:(1)因为 平面
平面 ,所以
,所以 是
是 在平面
在平面 内的射影,要证
内的射影,要证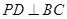 ,只要证
,只要证 ,连结
,连结 ,由题设易知三角形
,由题设易知三角形 为正三角形,而
为正三角形,而 是其边
是其边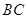 上的中线,所以
上的中线,所以 .
.
(2)由(1)知, ,而且
,而且 ,可以发现
,可以发现 为二面角
为二面角 的平面角,再利用直角姑角形
的平面角,再利用直角姑角形 求其大小;
求其大小;
(3)取 中点
中点 ,连结
,连结 易证
易证 ,
, 与
与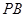 所成的角就是
所成的角就是 与
与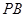 的成的角;先利用勾股定理求出
的成的角;先利用勾股定理求出 ,再用余弦定理求解.
,再用余弦定理求解.
试题解析:解答一:(1)在菱形 中,连接
中,连接 则
则 是等边三角形。
是等边三角形。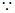 点
点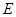 是边
是边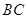 的中点
的中点
 平面
平面
 是斜线
是斜线 在底面
在底面 内的射影
内的射影

(2)
菱形 中,
中,

又 平面
平面 ,
, 是
是 在平面
在平面 内的射影
内的射影
 为二面角
为二面角 的平面角
的平面角
在菱形 中,
中, ,由(1)知,
,由(1)知, 等边三角形
等边三角形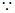 点
点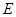 是
是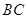 边的中点,
边的中点, 与
与 互相平分
互相平分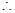 点
点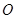 是
是 的重心
的重心
又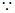

练习册系列答案
相关题目
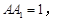
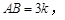
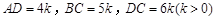 .
.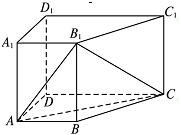
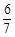 ,求k的值.
,求k的值.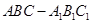 中,平面
中,平面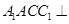 平面ABC,
平面ABC,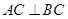 ,
,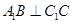 ,
,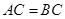 .
.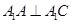 ;
;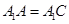 ,求二面角
,求二面角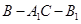 的余弦值.
的余弦值.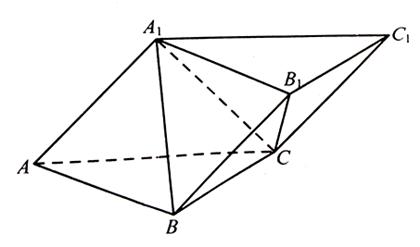
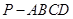 中,底面
中,底面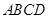 为矩形,侧棱
为矩形,侧棱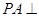 底面
底面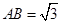 ,
,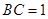 ,
,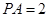 ,
, 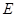 为
为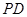 的中点.
的中点.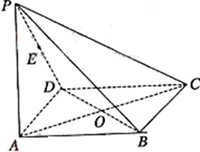
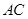 与
与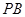 所成角的余弦值;
所成角的余弦值;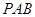 内找一点
内找一点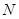 ,使
,使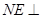 面
面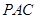 ,并求出点
,并求出点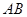 和
和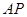 的距离.
的距离.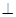 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD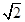 ,M为棱PB的中点.
,M为棱PB的中点.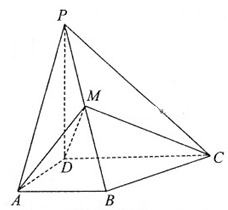
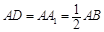 ,点E是棱AB上一点.且
,点E是棱AB上一点.且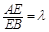 .
.
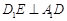 ;
;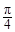 ,求
,求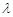 的值.
的值.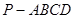 中,底面
中,底面 为平行四边形,
为平行四边形,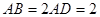 ,
,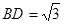 ,
,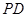 ⊥底面
⊥底面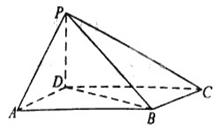
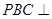 平面
平面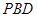 ;
; 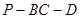 为
为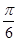 ,求
,求 与平面
与平面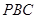 所成角的正弦值.
所成角的正弦值.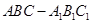 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是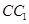 棱的中点,AE交
棱的中点,AE交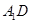 于点H.
于点H.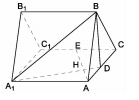
 平面
平面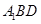 ;
;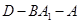 的余弦值;
的余弦值;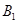 到平面
到平面