题目内容
设椭圆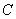 :
: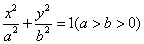 的离心率
的离心率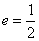 ,右焦点到直线
,右焦点到直线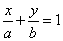 的距离
的距离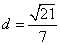 ,
, 为坐标原点。
为坐标原点。
(Ⅰ) 求椭圆 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆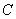 交于
交于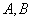 两点,以
两点,以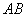 为直径的圆过原点
为直径的圆过原点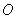 ,求
,求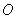 到直线
到直线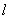 的距离。
的距离。
解:(Ⅰ) ,右焦点
,右焦点 到直线
到直线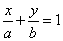 的距离
的距离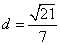 ,
,
则 ,且
,且 ,所以
,所以 ,
,
所以椭圆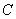 的的方程是:
的的方程是:
(Ⅱ)设直线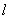 :
: ,那么:
,那么: ,
,
则 ,
,
又因为直线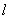 与椭圆
与椭圆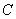 交于
交于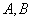 两点,以
两点,以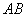 为直径的圆过原点
为直径的圆过原点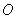 ,
,
 ,
,
 ,化简得
,化简得 ,即
,即
所以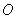 到直线
到直线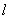 的距离为
的距离为

练习册系列答案
相关题目
题目内容
设椭圆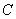 :
: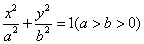 的离心率
的离心率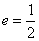 ,右焦点到直线
,右焦点到直线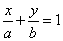 的距离
的距离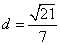 ,
,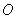 为坐标原点。
为坐标原点。
(Ⅰ) 求椭圆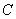 的方程;
的方程;
(Ⅱ)若直线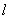 与椭圆
与椭圆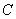 交于
交于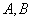 两点,以
两点,以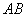 为直径的圆过原点
为直径的圆过原点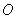 ,求
,求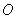 到直线
到直线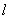 的距离。
的距离。
解:(Ⅰ) ,右焦点
,右焦点 到直线
到直线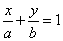 的距离
的距离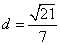 ,
,
则 ,且
,且 ,所以
,所以 ,
,
所以椭圆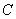 的的方程是:
的的方程是:
(Ⅱ)设直线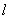 :
: ,那么:
,那么: ,
,
则 ,
,
又因为直线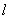 与椭圆
与椭圆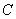 交于
交于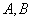 两点,以
两点,以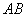 为直径的圆过原点
为直径的圆过原点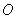 ,
,
 ,
,
 ,化简得
,化简得 ,即
,即
所以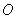 到直线
到直线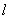 的距离为
的距离为
