题目内容
【题目】已知
的展开式中，前三项系数的绝对值成等差数列.
（1）求
；
（2）求第三项的二项式系数及展开式中
的系数；
（3）求展开式中系数的绝对值最大的项.
【答案】（1）
（2）
；
（3）
或
【解析】
(1)根据等差数列的知识及二项式系数的性质，列式求得n ；
(2)直接求解第三项的二项式系数，然后写出二项展开式的通项，由
的指数为
求得
,则展开式中的系数可求；
(3)根据二项式系数的性质，求得二项式系数最大的项.
(1)二项式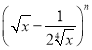
的展开式中，前三项系数的绝对值成等差数列，则
，解得：
(舍去)或；
(2)由(1)可得：
，
所以展开式中第三项的二项式系数为
，
展开式的通项为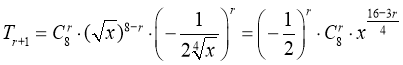
，
令
，解得
，
所以展开式中的系数为
；
(3)由(2)可得：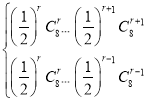
，解得
，
所以展开式中系数的绝对值最大的项为
或
.
练习册系列答案
阅读快车系列答案
相关题目
