题目内容
若0≤sinα≤
,则α的取值范围是
| ||
| 2 |
[2kπ,
+2kπ]∪[
+2kπ,π+2kπ],(k∈Z)
| π |
| 4 |
| 3π |
| 4 |
[2kπ,
+2kπ]∪[
+2kπ,π+2kπ],(k∈Z)
.| π |
| 4 |
| 3π |
| 4 |
分析:作出函数y=sinx在区间[0,2π]上的图象,利用正弦函数的单调性与特殊角的正弦值得到满足0≤sinx≤
的x的取值范围为[0,
]∪[
,π],结合正弦函数的周期为2π,可得当x∈R时不等式0≤sinx≤
的解集.由此即可得到满足题中不等式的角α的取值范围.
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
解答:解: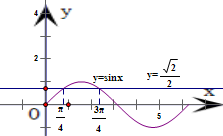 作出函数y=sinx在区间[0,2π]上的图象,如图所示.
作出函数y=sinx在区间[0,2π]上的图象,如图所示.
∵当x∈[0,π]时,sinx≥0.函数y=sinx在区间(0,
)上为增函数;在区间(
,π)上为减函数,
∴由sin
=sin
=
,可得在区间[0,2π]满足0≤sinx≤
的
x的取值范围为[0,
]∪[
,π],
根据函数y=sinx的周期为2π,得在R上满足0≤sinx≤
的x的取值范围为[2kπ,
+2kπ]∪[
+2kπ,π+2kπ],(k∈Z).
因此,满足不等式0≤sinα≤
的α取值范围是[2kπ,
+2kπ]∪[
+2kπ,π+2kπ],(k∈Z).
故答案为:[2kπ,
+2kπ]∪[
+2kπ,π+2kπ],(k∈Z)
 作出函数y=sinx在区间[0,2π]上的图象,如图所示.
作出函数y=sinx在区间[0,2π]上的图象,如图所示.∵当x∈[0,π]时,sinx≥0.函数y=sinx在区间(0,
| π |
| 2 |
| π |
| 2 |
∴由sin
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
x的取值范围为[0,
| π |
| 4 |
| 3π |
| 4 |
根据函数y=sinx的周期为2π,得在R上满足0≤sinx≤
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
因此,满足不等式0≤sinα≤
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
故答案为:[2kπ,
| π |
| 4 |
| 3π |
| 4 |
点评:本题给出三角不等式,求满足条件的角α的取值范围.着重考查了三角函数的图象与性质、特殊角的三角函数值与三角函数的周期性等知识,属于中档题.

练习册系列答案
相关题目
若圆中一段弧长正好等于该圆外切正三角形的边长,设这段弧所对的圆心角是θ,则sinθ的值所在的区间为( )
A、(-
| ||||
B、(0,
| ||||
C、(
| ||||
D、(-1,-
|