题目内容
设集合A={3,sinα},B={2,cosα},若A∩B={-
| ||
| 2 |
分析:由集合A与B的交集的定义可知,元素-
属于集合A且属于集合B,得到sinα与cosα相等都等于-
,根据α的范围,利用特殊角的三角函数值即可求出α的值.
| ||
| 2 |
| ||
| 2 |
解答: 解:由A∩B={-
解:由A∩B={-
},得到-
∈A且-
∈B,
又集合A={3,sinα},B={2,cosα},所以sinα=cosα=-
,
由α∈[0,2π],根据题意画出图象,如图所示:
根据图象得到α=
.
故答案为:
 解:由A∩B={-
解:由A∩B={-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
又集合A={3,sinα},B={2,cosα},所以sinα=cosα=-
| ||
| 2 |
由α∈[0,2π],根据题意画出图象,如图所示:
根据图象得到α=
| 5π |
| 4 |
故答案为:
| 5π |
| 4 |
点评:此题考查学生掌握交集的定义,根据角度的范围灵活运用特殊角的三角函数值化简求值,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
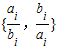 ≠min
≠min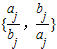 (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( ) ≠min
≠min (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( ) ≠min
≠min (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )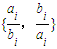 ≠min
≠min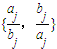 (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )