题目内容
已知函数 在(0,+∞)上的最小值是
在(0,+∞)上的最小值是 (n∈N+)).
(n∈N+)).
(1).求数列{ }的通项公式.
}的通项公式.
(2).证明: <
< .
.
(3).在点列 …….中是否存在两点Ai ,Aj 其中i, j∈N+ .,使直线AiAj的斜率为1,若存在,求出所有数对i, j .,若不存在,说明理由.
…….中是否存在两点Ai ,Aj 其中i, j∈N+ .,使直线AiAj的斜率为1,若存在,求出所有数对i, j .,若不存在,说明理由.
解:(1).由f (x)=2n -x,得
-x,得 =
= ……………1分.
……………1分.
令 =0,得x=
=0,得x= ……………………2分.
……………………2分.
当x∈(0 ,  ).时,
).时, <0.当x∈ (
<0.当x∈ ( ,+∞)时,
,+∞)时, >0.
>0.
∴f (x )在0,+∞.上有极小值f ( ) =
) = .
.
∴数列{an}的通项公式an= …………………………………5分.
…………………………………5分.
(2).∵
 ………………………6分..
………………………6分..
∴ =
=
 ………………8分.
………………8分.
(3).依题意,设Ai2i , ai.,Aj2j , aj.其中i, j∈N+ .是点列中的任意两点,则经过这两点的直线的斜率是:k=
 ……………………9分.
……………………9分.

 =1……………………11分.
=1……………………11分.
∴不存在这样的点列,使直线AiAj的斜率为1……………………12分..

练习册系列答案
相关题目
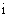 是虚数单位,
是虚数单位,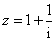 ,则
,则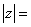
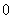 B.
B. 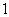 C.
C. 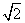 D.
D. 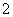
 ,tanβ=﹣
,tanβ=﹣ ,且0<α<
,且0<α< ,
, ,且
,且 ,
, .给出下列命题:
.给出下列命题: ,则
,则 ;②若
;②若 ,则
,则 ;③若
;③若 )的部分图象,点A为函数f(x)在y轴右侧的第一个零点,点B在函数f(x)图象上,它的纵坐标为1,直线AB的倾斜角等于____.
)的部分图象,点A为函数f(x)在y轴右侧的第一个零点,点B在函数f(x)图象上,它的纵坐标为1,直线AB的倾斜角等于____.
 是两条不同的直线,
是两条不同的直线, 是一个平面,且
是一个平面,且 ∥
∥ ,则
,则 ,则
,则 D.若
D.若 ,若
,若 恒成立,则实数a的取值范围
恒成立,则实数a的取值范围 B.
B. C.
C. D.
D.
 .
.