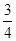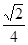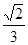题目内容
(本小题满分12分)
设△ABC的内角A、B、C的对边长分别为a、b、c, ,
, ,求B.
,求B.
设△ABC的内角A、B、C的对边长分别为a、b、c,
 ,
, ,求B.
,求B.:由 及
及 得
得
 ,
,
展开得
即
又由 =ac及正弦定理得.s
=ac及正弦定理得.s
故 ,
, 或
或 (舍去),
(舍去),
于是 或
或
又由 知
知 或
或
所以 .
. 

 及
及 得
得 ,
,展开得

即

又由
 =ac及正弦定理得.s
=ac及正弦定理得.s
故
 ,
, 或
或 (舍去),
(舍去),于是
 或
或
又由
 知
知 或
或
所以
 .
. 

:因为 中有三个角,为较减少角的个数,即化简该式子,需要利用三角形内角和定理
中有三个角,为较减少角的个数,即化简该式子,需要利用三角形内角和定理 实现转化.因为要求的结论是角
实现转化.因为要求的结论是角 ,需要利用正弦定理把把边化为角,然后联立求解即可.
,需要利用正弦定理把把边化为角,然后联立求解即可.
 中有三个角,为较减少角的个数,即化简该式子,需要利用三角形内角和定理
中有三个角,为较减少角的个数,即化简该式子,需要利用三角形内角和定理 实现转化.因为要求的结论是角
实现转化.因为要求的结论是角 ,需要利用正弦定理把把边化为角,然后联立求解即可.
,需要利用正弦定理把把边化为角,然后联立求解即可.
练习册系列答案
相关题目
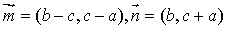 ,若
,若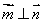 ,则角A的大小为( )
,则角A的大小为( )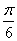
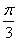
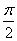
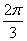
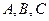 的对边分别为
的对边分别为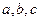 ,且满足
,且满足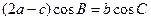 . (Ⅰ)求角B的大小; (Ⅱ)设
. (Ⅰ)求角B的大小; (Ⅱ)设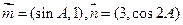 ,试求
,试求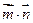 的取值范围.
的取值范围.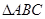 中,
中,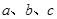 分别为内角
分别为内角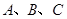 的对边,且
的对边,且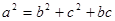
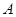 的大小;
的大小;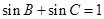 ,试求内角B、C的大小.
,试求内角B、C的大小. 船在灯塔
船在灯塔 北偏东
北偏东 且
且 ,
, 船在灯塔
船在灯塔 且
且 ,则
,则 两船的距离为( )
两船的距离为( )



 中,
中, 为其锐角,且
为其锐角,且 与
与 是方程
是方程 的两个根。
的两个根。 的值;
的值; 在
在 时的最大值及取得最大值时
时的最大值及取得最大值时 的取值.
的取值.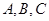 的对边分别为
的对边分别为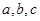 ,若
,若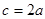 ,则
,则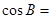 ( )
( )