题目内容
已知函数![]()
(1)若![]() 有两个不同的极值点,求a的取值范围;
有两个不同的极值点,求a的取值范围;
(2)当![]() 时,
时,![]() 表示函数
表示函数![]() 上的最大值,求
上的最大值,求![]() 的表达式;
的表达式;
(3)求证:![]() 。
。
【考点分析】本小题主要考查导数的运算法则,利用导数研究函数的单调性、极值、不等式的证明等基础知识,考查运算能力以及分类讨论的数学思想方法.
解:(1)(法一)![]()
设![]() ,
,![]() ,当
,当![]() 时
时![]()
若![]() ,由
,由![]() ,易知
,易知![]() 在
在![]() 时恒成立,无极值点.
时恒成立,无极值点.
若![]() ,设
,设![]() 的两根为
的两根为![]() 且
且![]() 。
。
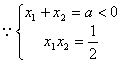 ,
,![]() ,故有
,故有
|
|
|
|
|
|
|
|
|
| 0 | - | 0 | + |
∴当![]() 时,函数
时,函数![]() 有两个极值点。…………4分
有两个极值点。…………4分
(法二)![]() ………1分
………1分
设![]() ,
,![]() 有两个极值点
有两个极值点![]()
![]() 有两个大于
有两个大于![]() 的不等实根
的不等实根![]() ,
,![]()
![]()

![]() ∴当
∴当![]() 时,函数
时,函数![]() 有两个极值点。…………4分
有两个极值点。…………4分
(2)当![]() 时,由(1)知
时,由(1)知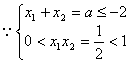 ,
,![]()
![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
![]() 在
在![]() 上的的最大值为
上的的最大值为![]() 或
或![]()
![]() ,设
,设![]() ,
,
![]() ,
,![]() ,故
,故![]() ,
,
![]()
![]() .
.
(3)由(2)知![]() 在
在![]() 上有最大值
上有最大值![]() ,且仅在
,且仅在![]() 时取得.取
时取得.取![]()
![]() ,
,![]() ,则
,则![]()
即![]()
![]()
法一:![]() ,
,![]() ,…,
,…,![]() ,
,![]() .
.
相加得:![]()
![]()
![]() ,
,
![]()
![]() ,
,
即:![]()
法二:用数学归纳法证明:
当![]() 时,易知成立,
时,易知成立,
假设当![]() 时,不等式成立,即
时,不等式成立,即![]()
![]() 成立
成立
![]() 时,
时,![]()
=![]()
=![]()
<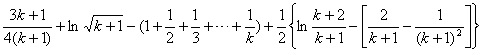
![]() (由归纳假设及
(由归纳假设及![]() ,
,![]() )
)
∴当![]() 不等式也成立,故得证。
不等式也成立,故得证。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的表达式;
的表达式; 上是单调函数.
上是单调函数.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 ,求
,求 的零点;
的零点; 上有两个不同的零点,求
上有两个不同的零点,求 的取值范围。
的取值范围。