题目内容
(本小题满分12分)求与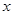 轴相切,圆心在直线
轴相切,圆心在直线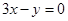 上,且被直线
上,且被直线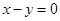 截得的弦长为
截得的弦长为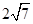 的圆的方程。
的圆的方程。
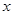 轴相切,圆心在直线
轴相切,圆心在直线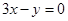 上,且被直线
上,且被直线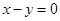 截得的弦长为
截得的弦长为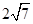 的圆的方程。
的圆的方程。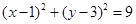 或
或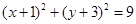 。
。本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键,属于中档题
设圆心坐标,写出圆的方程,然后利用圆心到直线的距离得到半径,从而解得。
解:设所求的方程为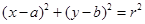
则圆心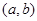 到直线
到直线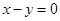 的距离为
的距离为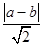
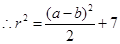 ,即
,即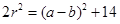 (1) ----4分
(1) ----4分
由于所求圆和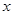 轴相切,
轴相切,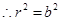 (2) ----2分
(2) ----2分
又圆心在直线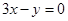 上,
上,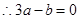 (3) ----2分
(3) ----2分
联立(1)(2)(3)解得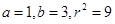 或
或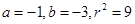 ----10分
----10分
故所求圆的方程是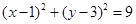 或
或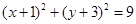 ------12分
------12分
设圆心坐标,写出圆的方程,然后利用圆心到直线的距离得到半径,从而解得。
解:设所求的方程为
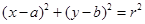
则圆心
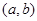 到直线
到直线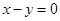 的距离为
的距离为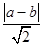
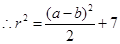 ,即
,即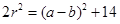 (1) ----4分
(1) ----4分由于所求圆和
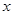 轴相切,
轴相切,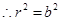 (2) ----2分
(2) ----2分又圆心在直线
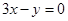 上,
上,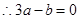 (3) ----2分
(3) ----2分联立(1)(2)(3)解得
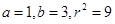 或
或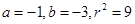 ----10分
----10分故所求圆的方程是
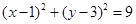 或
或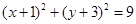 ------12分
------12分
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
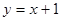 上的一点向圆
上的一点向圆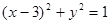 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )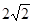
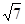
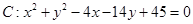 及点
及点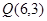 .
.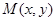 为圆
为圆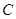 上任一点,求
上任一点,求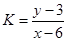 的最大值和最小值;
的最大值和最小值;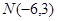 ,直线
,直线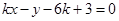 与圆C交于点A、B.当
与圆C交于点A、B.当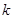 为何值时
为何值时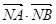 取到最小值。
取到最小值。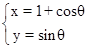 (θ为参数)的圆心到直线l:
(θ为参数)的圆心到直线l: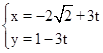 (t为参数)的距离为 .
(t为参数)的距离为 .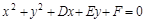 与
与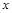 轴的两个交点分别位于原点的两侧,则有( )
轴的两个交点分别位于原点的两侧,则有( )
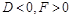


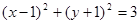 ,则此圆的圆心和半径分别为( )
,则此圆的圆心和半径分别为( ) ,
,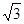
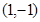 ,
, 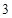
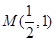 的直线
的直线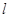 与圆C:
与圆C: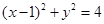 交于
交于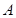 、
、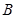 两点,
两点,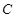 为圆心,当
为圆心,当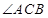 最小时,直线
最小时,直线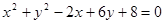 的圆心和半径分别是
的圆心和半径分别是 ,2
,2
 2
2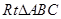 的两条直角边
的两条直角边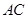 ,
,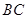 的长分别为
的长分别为 ,
,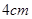 ,以
,以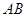 交于点
交于点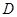 ,则
,则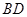 =
=