题目内容
已知函数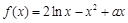 (
(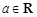 ).
).
(1)当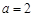 时,求
时,求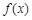 的图象在
的图象在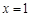 处的切线方程;
处的切线方程;
(2)若函数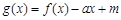 在
在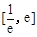 上有两个零点,求实数
上有两个零点,求实数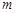 的取值范围;
的取值范围;
(3)若函数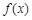 的图象与
的图象与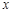 轴有两个不同的交点
轴有两个不同的交点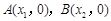 ,且
,且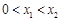 ,求证:
,求证: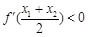 (其中
(其中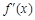 是
是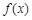 的导函数).
的导函数).
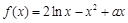 (
(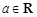 ).
).(1)当
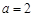 时,求
时,求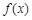 的图象在
的图象在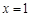 处的切线方程;
处的切线方程;(2)若函数
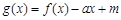 在
在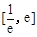 上有两个零点,求实数
上有两个零点,求实数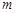 的取值范围;
的取值范围;(3)若函数
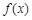 的图象与
的图象与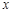 轴有两个不同的交点
轴有两个不同的交点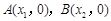 ,且
,且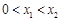 ,求证:
,求证: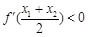 (其中
(其中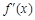 是
是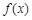 的导函数).
的导函数).(1)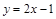 ;(2)
;(2)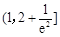 ;(3)证明见解析.
;(3)证明见解析.
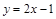 ;(2)
;(2)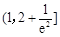 ;(3)证明见解析.
;(3)证明见解析.试题分析:解题思路:(1)利用导数的几何意义求解即可;(2)利用该区间上的极值的正负判断函数零点的个数;(3)通过构造函数求最值进行证明.规律总结:利用导数研究函数的性质是常见题型,主要是通过导数研究函数的单调性、求单调区间、求极值、最值以及不等式恒成立等问题,往往计算量较大,思维量大,要求学生有较高的逻辑推理能力.
试题解析:(1)当
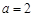 时,
时, ,
,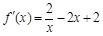 ,切点坐标为
,切点坐标为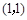 ,
,切线的斜率
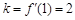 ,则切线方程为
,则切线方程为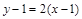 ,即
,即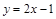 .
.(2)
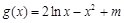 ,则
,则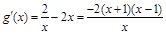 ,
,因
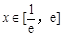 ,故
,故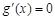 时,
时,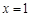 .当
.当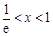 时,
时,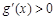 ;当
;当 时,
时, .
.所以
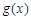 在
在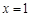 处取得极大值
处取得极大值 .
.又
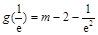 ,
,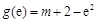 ,
,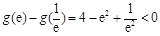 ,则
,则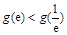 ,
,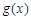 在
在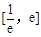 上有两个零点,则
上有两个零点,则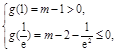
解得
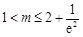 ,即实数
,即实数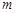 的取值范围是
的取值范围是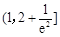 .
.(3)因为
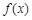 的图象与
的图象与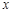 轴交于两个不同的点
轴交于两个不同的点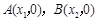 ,
,所以方程
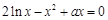 的两个根为
的两个根为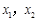 ,则
,则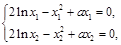 两式相减得
两式相减得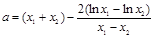 .又
.又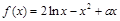 ,
,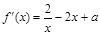 ,则
,则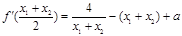
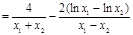 .
.下证
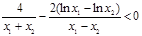 (*),即证明
(*),即证明 ,
,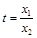 ,
,因为
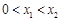 ,∴
,∴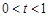 ,即证明
,即证明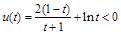 在
在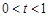 上恒成立.
上恒成立.所以
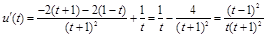 ,又
,又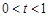 ,∴
,∴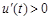 ,
,所以
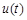 在
在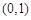 上是增函数,则
上是增函数,则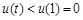 ,从而知
,从而知 ,
,故(*)式成立,即
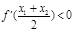 成立.
成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
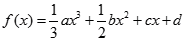 的图像过原点,且在点
的图像过原点,且在点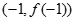 处的切线与
处的切线与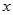 轴平行,对任意
轴平行,对任意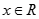 ,都有
,都有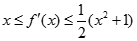 .
.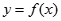 在点
在点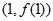 处切线的斜率;
处切线的斜率;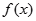 的解析式;
的解析式;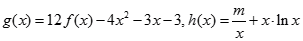 ,对任意
,对任意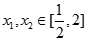 ,都有
,都有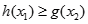 .求实数
.求实数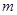 的取值范围.
的取值范围.
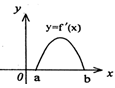
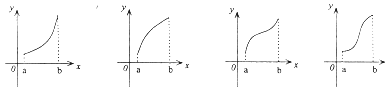
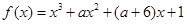 有极大值和极小值,则实数
有极大值和极小值,则实数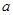 的取值范围是
的取值范围是 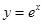 在
在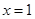 处的切线的斜率为 .
处的切线的斜率为 .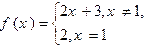 ,则下面结论错误的个数是( )
,则下面结论错误的个数是( )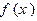 在
在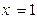 处连续 (2)
处连续 (2)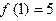 (3)
(3)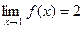 (4)
(4)