题目内容
已知椭圆
+y2=1与双曲线
-3y2=1具有相同的焦点F1，F2，点P是两曲线的公共点，则∠F1PF2= ．
| x2 |
| a2 |
| x2 |
| b2 |
考点：双曲线的简单性质,椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由椭圆和双曲线的焦点相同得到a2-1=b2+
，再由定义列方程求得P到两焦点的距离，然后利用余弦定理求解．
| 1 |
| 3 |
解答：
解：如图，
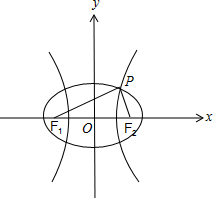
由题意可得，a2-1=b2+
，
|PF1|+|PF2|=2a，|PF1|-|PF2|=2b，
则|PF1|=a+b，
|PF2|=a-b，
cos∠F1PF2=
=
=
．
∴∠F1PF2=
．
故答案为：
．
由题意可得，a2-1=b2+
| 1 |
| 3 |
|PF1|+|PF2|=2a，|PF1|-|PF2|=2b，
则|PF1|=a+b，
|PF2|=a-b，
cos∠F1PF2=
| |PF1|2+|PF2|2-|F1F2|2 |
| 2|PF1||PF2| |
=
| (a+b)2+(a-b)2-4a2+4 |
| 2a2-2b2 |
=
| 1 |
| 2 |
∴∠F1PF2=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查了椭圆与双曲线的简单几何性质，涉及圆锥曲线上的点与两焦点连线构成的三角形问题，常用圆锥曲线的定义及余弦定理求解，是中档题．
练习册系列答案
相关题目
已知数列{an}的前n项之和是Sn，且4Sn=（an+1）2，则下列说法正确的是（ ）
| A、数列{an}为等差数列 |
| B、数列{an}为等比数列 |
| C、数列{an}为等差或等比数列 |
| D、数列{an}可能既不是等差数列也不是等比数列 |
△ABC与A1、B1、C1不在同一平面内，如果三条直线AA1，BB1，CC1，两两相交，求证：AA1，BB1，CC1交于一点．