题目内容
△ABC的内角A，B，C的对边分别为a，b，c.已知3acos C＝2ccos A，tan A＝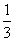
，求B.
解：由题设和正弦定理得
3sin Acos C＝2sin Ccos A，
故3tan Acos C＝2sin C.
因为tan A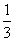＝，所以cos C＝2sin C，
所以tan C＝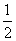
.
所以tan B＝tan[180°－(A＋C)]
＝－tan(A＋C)
＝
＝－1，
所以B＝135°.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
,
.若方程
有两个不相等的实根，则实数k的取值范围是
B. 
C.
D. 
的最小正周期是( )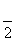
B．π C．2π D．4π
是减函数，则a的取值范围是________．
＝________．
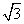，cos2A－cos2B＝
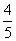，求△ABC的面积．
＝( )
B.
，比较
与
的大小．