Question

甲、乙两地相距s km，汽车从甲地匀速行驶到乙地，速度不得超过c km/h，已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度v( km/h)的平方成正比，比例系数为b；固定部分为a元.

(1)把全程运输成本y(元)表示为速度v( km/h)的函数，并指出这个函数的定义域；

(2)为了使全程运输成本最小，汽车应以多大速度行驶？

Answer 1

解：(1)依题意，汽车从甲地匀速行驶到乙地所用的时间为，全程运输成本为

y＝a·＋bv²·＝s(＋bv)，故所求函数及其定义域为y＝s(+bv)，v∈(0，c］.

(2)依题意，知s、a、b、v都为正数，故有s(＋bv)≥2s，当且仅当＝bv，

即v＝时，上式中等号成立.

若≤c，则当v＝时，全程运输成本y最小.

若＞c，当v∈(0，c］时，有

s(＋bv)－s(＋bc)＝s·［a()＋b(v－c)］＝(c－v)(a－bcv).

因为c－v≥0，且a＞bc²，故a－bcv＞a－bc²＞0.

所以s(＋bv)≥s(＋bc)，当且仅当v＝c时等号成立，也即v＝c时，全程运输成本y最小.

综上知，为使全程运输成本y最小，当≤c时，行驶速度应为v＝；当＞c时，行驶速度应为v＝c.

点评：(1)抓住基本关系：全程成本=每小时成本×时间，成本＝可变成本＋固定成本，求最值时要注意变量的定义域.

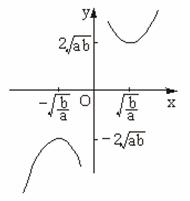
(2)函数y=ax+(a、b∈R⁺)的图象如下图所示.