题目内容
已知函数![]()
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)求证:当a>l时,f(x)存在极值,且所有的极值之和小于-3.
答案:
解析:
解析:
|
解:(Ⅰ) (1)当 (2)当 (3)当 (4)当 (Ⅱ)由(Ⅰ)可得 所以所有极值之和为 设 = 当 所以 |

练习册系列答案
相关题目


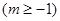 .
.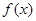 的单调性;
的单调性;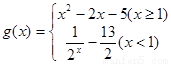 .当
.当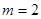 时,若对任意
时,若对任意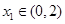 ,
,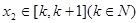 ,使
,使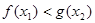 ,求实数
,求实数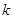 的最小值
的最小值 .
.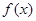 的奇偶性;
的奇偶性; 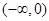 上的单调性并用定义证明.
上的单调性并用定义证明.