题目内容
(本题满分14分)
已知函数 .
.
(Ⅰ) 讨论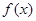 的奇偶性;
的奇偶性;
(Ⅱ)判断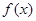 在
在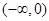 上的单调性并用定义证明.
上的单调性并用定义证明.
【答案】
(Ⅰ) 当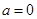 时,
时, 为奇函数;当
为奇函数;当 时,
时, 不具备奇偶性
不具备奇偶性
(Ⅱ)证明略
【解析】(Ⅰ)函数 的定义域为
的定义域为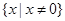 关于原点对称. ……………1分
关于原点对称. ……………1分
方法1、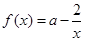 ,
,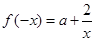 …………………………2分
…………………………2分
若 ,则
,则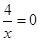 ,无解, ∴
,无解, ∴ 不是偶函数; …………………4分
不是偶函数; …………………4分
若 ,则
,则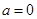 ,显然
,显然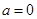 时,
时, 为奇函数……………………6分
为奇函数……………………6分
综上,当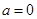 时,
时, 为奇函数;当
为奇函数;当 时,
时, 不具备奇偶性. ………7分
不具备奇偶性. ………7分
方法2、函数 的定义域为
的定义域为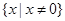 关于原点对称. ……………1分
关于原点对称. ……………1分
当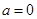 时,
时,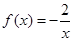 ,
,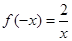 ,∴
,∴ ,
,
∴ 为奇函数; ………………………………………………4分
为奇函数; ………………………………………………4分
当 时,
时,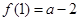 ,
,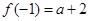 ,显然
,显然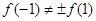
∴ 不具备奇偶性. …………………………………………7分
不具备奇偶性. …………………………………………7分
(Ⅱ)函数 在
在 上单调递增; ………………………8分
上单调递增; ………………………8分
证明:任取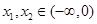 且
且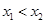 ,则
,则
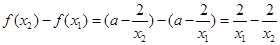
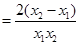 ……………11分
……………11分
∵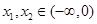 且
且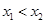 , ∴
, ∴ ,
,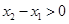 ,
,
从而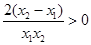 , 故
, 故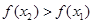 ,…………………………13分
,…………………………13分
∴ 在
在 上单调递增. ………………………………14分
上单调递增. ………………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).