题目内容
设数列 的前
的前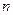 项和为
项和为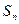 ,且满足
,且满足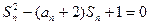 ,
,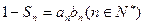 .
.
(Ⅰ)求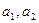 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若正项数列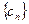 满足
满足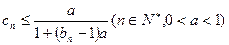 ,
,
求证: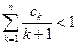 .
.
 的前
的前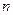 项和为
项和为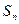 ,且满足
,且满足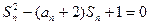 ,
,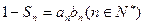 .
.(Ⅰ)求
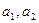 的值;
的值;(Ⅱ)求数列
 的通项公式;
的通项公式;(Ⅲ)若正项数列
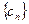 满足
满足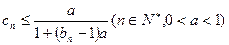 ,
,求证:
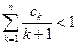 .
.(Ⅰ) 
 (Ⅱ)
(Ⅱ)  (Ⅲ)见解析
(Ⅲ)见解析

 (Ⅱ)
(Ⅱ)  (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ)
 ………………………………………………3分
………………………………………………3分
(Ⅱ) ………………………①
………………………①
当 时,
时,  代入①式得
代入①式得 ………②……………5分
………②……………5分
由 (Ⅰ) 知
猜想 ……………………………………………………………………………6分
……………………………………………………………………………6分
下面用数学归纳法证明猜想
(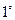 )
) 已证明;
已证明;
( )假设
)假设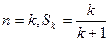
则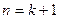 时,
时,
 成立
成立
综合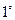 ,
, 猜想成立.
猜想成立.
∴当 时,
时, 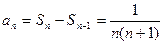 ,当
,当 时也满足,故
时也满足,故
………………………………………………………………………………………………9分
(Ⅲ)由(Ⅱ)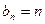 ,
,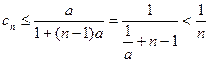 ,则
,则
 ……………………………………………………13分
……………………………………………………13分

 ………………………………………………3分
………………………………………………3分(Ⅱ)
 ………………………①
………………………①当
 时,
时,  代入①式得
代入①式得 ………②……………5分
………②……………5分由 (Ⅰ) 知

猜想
 ……………………………………………………………………………6分
……………………………………………………………………………6分下面用数学归纳法证明猜想
(
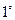 )
) 已证明;
已证明;(
 )假设
)假设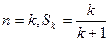
则
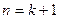 时,
时,
 成立
成立综合
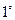 ,
, 猜想成立.
猜想成立. ∴当
 时,
时, 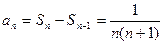 ,当
,当 时也满足,故
时也满足,故
………………………………………………………………………………………………9分
(Ⅲ)由(Ⅱ)
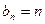 ,
,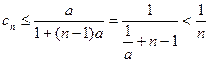 ,则
,则 ……………………………………………………13分
……………………………………………………13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
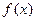 ,存在实数
,存在实数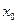 ,使得对于任意实数
,使得对于任意实数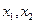 ,总有
,总有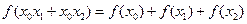 恒成立。
恒成立。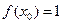 ,且对任意正整数
,且对任意正整数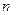 ,有
,有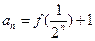 , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;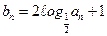 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列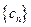 ,具体法则如下:
,具体法则如下: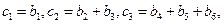
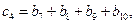 ……,求证:
……,求证: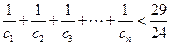 。
。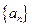 的前
的前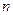 项和为
项和为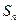 ,对任意的正整数
,对任意的正整数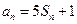 成立,记
成立,记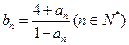 。
。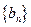 的通项公式;
的通项公式;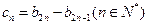 ,设数列
,设数列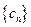 的前
的前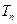 ,求证:对任意正整数
,求证:对任意正整数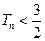 ;
;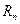 。已知正实数
。已知正实数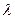 满足:对任意正整数
满足:对任意正整数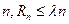 恒成立,求
恒成立,求 满足
满足 .
. 时,证明不等式:
时,证明不等式: .
.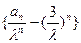 是等差数列,公差为2,
是等差数列,公差为2,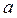 1,=11,
1,=11,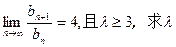 的值; (Ⅱ)在(Ⅰ)条件下,求数列{
的值; (Ⅱ)在(Ⅰ)条件下,求数列{ }的前n项和.
}的前n项和.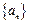 的前
的前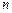 项和
项和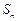 满足
满足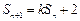 ,且
,且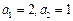

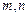 ,使
,使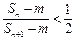 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.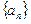 的公差为2,前
的公差为2,前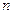 项和为
项和为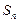 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )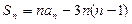
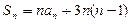
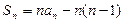
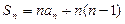
 }的前11项和为 ()
}的前11项和为 ()