题目内容
设函数 (其中
(其中 ),区间
),区间 .
.
(1)求区间 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 );
);
(2)把区间 的长度记作数列
的长度记作数列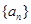 ,令
,令 ,证明:
,证明: .
.
 (其中
(其中 ),区间
),区间 .
.(1)求区间
 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 );
);(2)把区间
 的长度记作数列
的长度记作数列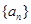 ,令
,令 ,证明:
,证明: .
.(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析试题分析:(1)由
 ,得
,得 ,解一元二次不等时即可.
,解一元二次不等时即可.(2)先利用裂项相消法求出
 =
= ,故
,故 ,又易知
,又易知 单调递增,故
单调递增,故 ,即可.
,即可.(1)由
 ,得
,得 ,解得
,解得 , 3分
, 3分即
 ,所以区间
,所以区间 的长度为
的长度为 ; 6分
; 6分(2)由(1)知
 , 7分
, 7分则

 10分
10分因为
 ,故
,故 , 11分
, 11分又易知
 单增,故
单增,故 ,
,综上
 . 12分
. 12分 的长度的定义;裂项相消法.
的长度的定义;裂项相消法.
练习册系列答案
相关题目
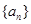 的前
的前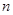 项和为
项和为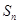 ,若
,若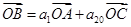 ,且
,且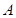 ,
,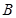 ,
,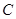 三点共线(该
三点共线(该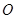 ),则
),则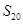 =_____________.
=_____________.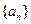 的公差大于零的等差数列,已知
的公差大于零的等差数列,已知 ,
, .
. 是以函数
是以函数 的最小正周期为首项,以
的最小正周期为首项,以 为公比的等比数列,求数列
为公比的等比数列,求数列 的前
的前 项和
项和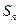 .
.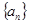 满足
满足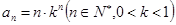 ,给出下列命题:
,给出下列命题: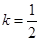 时,数列
时,数列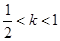 时,数列
时,数列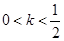 时,数列
时,数列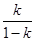 为正整数时,数列
为正整数时,数列 满足
满足 则
则 .
.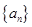 前15项的和
前15项的和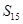 =30,则
=30,则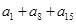 =___________.
=___________. 满足
满足 则其前11项和S11= .
则其前11项和S11= .