题目内容
已知数列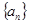 满足
满足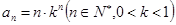 ,给出下列命题:
,给出下列命题:
①当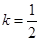 时,数列
时,数列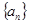 为递减数列
为递减数列
②当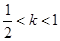 时,数列
时,数列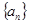 不一定有最大项
不一定有最大项
③当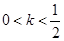 时,数列
时,数列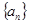 为递减数列
为递减数列
④当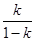 为正整数时,数列
为正整数时,数列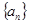 必有两项相等的最大项
必有两项相等的最大项
请写出正确的命题的序号____
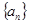 满足
满足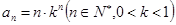 ,给出下列命题:
,给出下列命题:①当
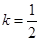 时,数列
时,数列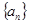 为递减数列
为递减数列②当
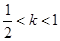 时,数列
时,数列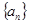 不一定有最大项
不一定有最大项③当
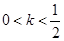 时,数列
时,数列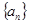 为递减数列
为递减数列④当
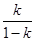 为正整数时,数列
为正整数时,数列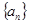 必有两项相等的最大项
必有两项相等的最大项请写出正确的命题的序号____
③④
选项①:当
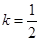 时,
时, ,有
,有 ,
, ,则
,则 ,即数列
,即数列 不是递减数列,故①错误;
不是递减数列,故①错误;选项②:当
 时,
时, ,因为
,因为 ,所以数列
,所以数列 可有最大项,故②错误;
可有最大项,故②错误;选项③:当
 时,
时, ,所以
,所以 ,即数列
,即数列 是递减数列,故③正确;
是递减数列,故③正确;选项④:
 ,当
,当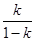 为正整数时,
为正整数时, ;当
;当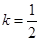 时,
时, ;当
;当 时,令
时,令 ,解得
,解得 ,
, ,数列
,数列 必有两项相等的最大项,故④正确.
必有两项相等的最大项,故④正确.所以正确的选项为③④.
【考点】数列的函数特征.

练习册系列答案
相关题目
 (其中
(其中 ),区间
),区间 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 );
);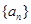 ,令
,令 ,证明:
,证明: .
. 同时满足:(1)各项均为正数,(2)存在常数k, 对任意
同时满足:(1)各项均为正数,(2)存在常数k, 对任意 都成立,那么,这样的数列
都成立,那么,这样的数列 , a2、a4、a5成等差数列,求的值;
, a2、a4、a5成等差数列,求的值; 对任意
对任意 都成立?若存在,求出λ;若不存在,说明理由.
都成立?若存在,求出λ;若不存在,说明理由.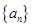 满足
满足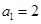 ,向量
,向量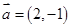 ,
,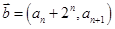 且
且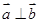 .
.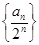 为等差数列,并求
为等差数列,并求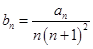 ,若对任意
,若对任意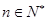 都有
都有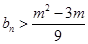 成立,求实数
成立,求实数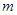 的取值范围.
的取值范围.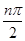 -bn·cos2
-bn·cos2