题目内容
已知 是定义在(-∞,+∞)上的奇函数,且满足
是定义在(-∞,+∞)上的奇函数,且满足
(1)求实数a,b,并确定函数f(x)的解析式
(2)用定义证明f(x)在(-1,1)上是增函数.
【答案】分析:(1)利用函数的奇偶性即可求出;
(2)利用函数的单调性即可证明.
解答:解:(1)由满足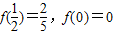 ,
,
∴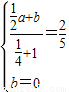 ,解得
,解得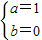 .
.
∴a=1,b=0,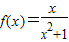 ;
;
(2)证明:设-1<x1<x2<1,
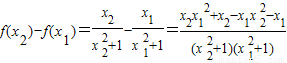 =
=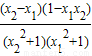 ,
,
∵-1<x1<x2<-1,∴-1<x1•x2<1,即1-x1x2>0,x2-x1>0,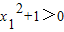 ,
,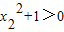 ,
,
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
所以函数f(x)在(-1,1)上是增函数.
点评:熟练掌握函数的奇偶性和单调性是解题的关键.
(2)利用函数的单调性即可证明.
解答:解:(1)由满足
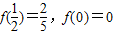 ,
,∴
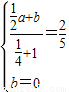 ,解得
,解得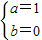 .
.∴a=1,b=0,
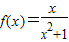 ;
;(2)证明:设-1<x1<x2<1,
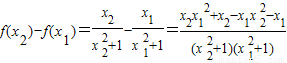 =
=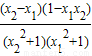 ,
,∵-1<x1<x2<-1,∴-1<x1•x2<1,即1-x1x2>0,x2-x1>0,
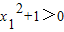 ,
,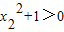 ,
,∴f(x2)-f(x1)>0,即f(x2)>f(x1).
所以函数f(x)在(-1,1)上是增函数.
点评:熟练掌握函数的奇偶性和单调性是解题的关键.

练习册系列答案
相关题目
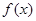 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意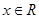 ,都有
,都有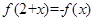 ,且当
,且当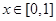 时在
时在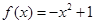 ,若
,若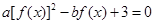 在
在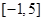 上有5个根
上有5个根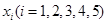 ,则
,则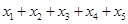 的值为( )
的值为( )