题目内容
14.若关于x的方程($\frac{1}{2}$)x=$\frac{1}{1-lga}$有正根,则实数a的取值范围是( )| A. | (0,1] | B. | (0,1) | C. | (1,10) | D. | [1,+∞) |
分析 先求出方程有解的范围,利用补集思想,先求出($\frac{1}{2}$)x=$\frac{1}{1-lga}$没有正根的等价条件即可得到结论.
解答 解:若($\frac{1}{2}$)x=$\frac{1}{1-lga}$有解,则$\frac{1}{1-lga}$>0,则1-lga>0,lga<1,即0<a<10,
若($\frac{1}{2}$)x=$\frac{1}{1-lga}$没有正根,
则x≤0时,方程有解,
∵($\frac{1}{2}$)x≥1,
∴$\frac{1}{1-lga}$≥1,则0<1-lga≤1,
即0≤lga<1,即1≤a<10,
则若关于x的方程($\frac{1}{2}$)x=$\frac{1}{1-lga}$有正根,
则0<a<1,
故选:B
点评 本题主要考查函数与方程的应用,根据指数函数的性质,利用正难则反的原则进行转化是解决本题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
2.已知双曲线$\frac{{x}^{2}}{k}+\frac{{y}^{2}}{6+k}=1$的实轴长为4,则双曲线的渐近线方程为( )
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
9.已知x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ y≥-1\\ 4x+y≤9\\ x+y≤3\end{array}\right.$,若目标函数z=mx+y(m>0)的最大值为1,则m的值是( )
| A. | $-\frac{20}{9}$ | B. | 1 | C. | 2 | D. | 5 |
3.5名同学参加庆祝抗日胜利70周年文艺演出,要求是甲乙必须相邻,而丙丁不能相邻,不同的排队方法的种数是( )
| A. | 48 | B. | 24 | C. | 20 | D. | 12 |
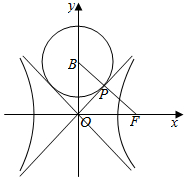 如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.
如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.