题目内容
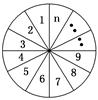
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
(1)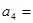 ;
;
(2)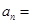 .
.

(1)
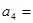 ;
;(2)
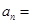 .
.(1)18;(2)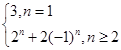 .
.
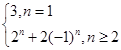 .
.试题分析:(1)设三种不同颜色分别为甲、乙、丙三种.
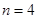 时,第1区域有3种选择, 第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以
时,第1区域有3种选择, 第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以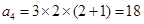 ;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第
;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第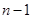 区域有2种染色方案.此时考虑第
区域有2种染色方案.此时考虑第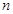 区域也有2种涂色方案,在此情况下有两种情况:
区域也有2种涂色方案,在此情况下有两种情况:情况一:第
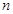 区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上
区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上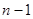 个区域涂色,即为
个区域涂色,即为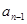 种染色方案;
种染色方案;情况二:第
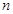 区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上
区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上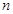 个区域染色,且相邻区域颜色互异,即此时的情况就是
个区域染色,且相邻区域颜色互异,即此时的情况就是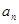 .根据分类原理可知
.根据分类原理可知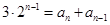 ,且满足初始条件:
,且满足初始条件: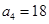 .
.即递推公式为
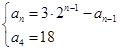 ,由
,由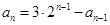 变形得
变形得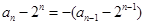 ,所以数列
,所以数列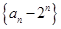 是以-1为公比的等比数列.所以
是以-1为公比的等比数列.所以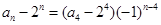 ,即
,即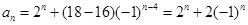 .当
.当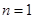 时,易知有3种染色方法,即
时,易知有3种染色方法,即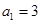 ,不满足上述通项公式;当
,不满足上述通项公式;当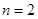 时,易知有
时,易知有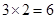 种染色方法,即
种染色方法,即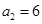 ,满足上述通项公式;当
,满足上述通项公式;当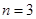 时,易知有
时,易知有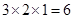 种染色方法,即
种染色方法,即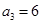 ,满足上述通项公式.
,满足上述通项公式.综上所述,
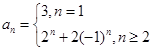 .
.
练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
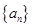 满足:
满足: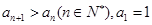 ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列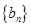 的前三项.
的前三项.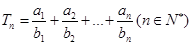 ,若
,若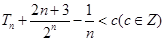 恒成立,求c的最小值.
恒成立,求c的最小值. 为等比数列,
为等比数列, 是等差数列,
是等差数列,
 的通项公式及前
的通项公式及前 项和
项和 ;
;
 ,
,
 ,其中
,其中 ,试比较
,试比较 与
与 的大小,并加以证明.
的大小,并加以证明.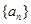 的前
的前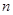 项和为
项和为 ,且
,且 .
. 求证:
求证: .
.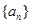 的前n项和为
的前n项和为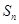 ,已知
,已知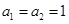 ,
,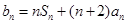 ,数列
,数列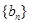 是公差为d的等差数列,
是公差为d的等差数列,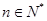 .
.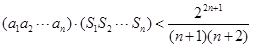 .
.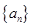 是正数组成的数列,
是正数组成的数列,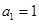 ,且点
,且点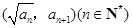 在函数
在函数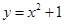 的图象上.
的图象上.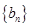 满足
满足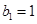 ,
,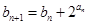 ,求证:
,求证:
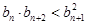 .
.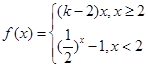 ,
,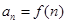 ,若数列
,若数列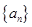 是单调递减数列,则实数
是单调递减数列,则实数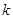 的取值范围为( )
的取值范围为( )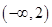
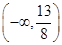
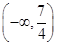
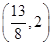
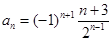 ,则该数列的第五项为( )
,则该数列的第五项为( )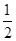
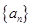 的首项为
的首项为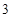 ,
,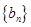 为等差数列且
为等差数列且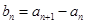 .若
.若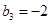 ,
,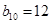 ,则
,则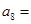 ( )
( )

