题目内容
若数列{an}的项构成的新数列{an+1-Kan}是公比为l的等比数列，则相应的数列{an+1-1an}是公比为k的等比数列，运用此性质，可以较为简洁的求出一类递推数列的通项公式，并简称此法为双等比数列法．已知数列{an}中，
，
，且
．（1）试利用双等比数列法求数列{an}的通项公式；
（2）求数列{an}的前n项和Sn．
【答案】分析：（1）利用
，判断
是公比为
的等比数列，求出
，然后求数列{an}的通项公式；
（2）利用拆项法，把通项分解为两个等比数列，然后求数列{an}的前n项和Sn．
解答：解：（1）有条件知：
，①
所以
是公比为
的等比数列，
故
是以首项为
，公比为
的等比数列，
所以：
，②
由①、②得
．
（2）Sn=a1+a2+…+an
═
+
+
=
=
．
点评：本题主要考查等比数列的判断，数列求和的拆项法、等比数列的前n项和公式．考查学生的运算能力．
，判断是公比为的等比数列，求出，然后求数列{an}的通项公式；（2）利用拆项法，把通项分解为两个等比数列，然后求数列{an}的前n项和Sn．
解答：解：（1）有条件知：
，①所以
是公比为的等比数列，故
是以首项为，公比为的等比数列，所以：
，②由①、②得
．（2）Sn=a1+a2+…+an
═
++=
=
．点评：本题主要考查等比数列的判断，数列求和的拆项法、等比数列的前n项和公式．考查学生的运算能力．
练习册系列答案
阅读快车系列答案
相关题目
，
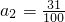，且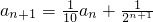
．