题目内容
设 (
( 是自然对数的底数,
是自然对数的底数, ),且
),且 .
.
(1)求实数 的值,并求函数
的值,并求函数 的单调区间;
的单调区间;
(2)设 ,对任意
,对任意 ,恒有
,恒有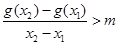 成立.求实数
成立.求实数 的取值范围;
的取值范围;
(3)若正实数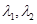 满足
满足 ,
, ,试证明:
,试证明: ;并进一步判断:当正实数
;并进一步判断:当正实数 满足
满足
 ,且
,且 是互不相等的实数时,不等式
是互不相等的实数时,不等式
 是否仍然成立.
是否仍然成立.
 (
( 是自然对数的底数,
是自然对数的底数, ),且
),且 .
.(1)求实数
 的值,并求函数
的值,并求函数 的单调区间;
的单调区间;(2)设
 ,对任意
,对任意 ,恒有
,恒有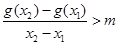 成立.求实数
成立.求实数 的取值范围;
的取值范围;(3)若正实数
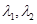 满足
满足 ,
, ,试证明:
,试证明: ;并进一步判断:当正实数
;并进一步判断:当正实数 满足
满足
 ,且
,且 是互不相等的实数时,不等式
是互不相等的实数时,不等式
 是否仍然成立.
是否仍然成立.(1)参考解析;(2) ;(3)成立,参考解析
;(3)成立,参考解析
 ;(3)成立,参考解析
;(3)成立,参考解析试题分析:(1)由
 (
( 是自然对数的底数,
是自然对数的底数, ),且
),且 ,即可求出
,即可求出 .再根据导函数的值即可求出单调区间.
.再根据导函数的值即可求出单调区间.(2)对任意
 ,恒有
,恒有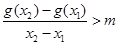 成立,通过去分母,整理成两个函数的单调性的问题即
成立,通过去分母,整理成两个函数的单调性的问题即 ,则
,则 在
在 上单调递增,又
上单调递增,又 ,再通过求导即可得到m的取值范围.
,再通过求导即可得到m的取值范围.(3)若正实数
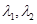 满足
满足 ,
, ,则
,则 .通过代入函数关系式消元再用基本不等式即可得到结论.当
.通过代入函数关系式消元再用基本不等式即可得到结论.当
 ,且
,且 是互不相等的实数时,不等式
是互不相等的实数时,不等式
 是否仍然成立.有数学归纳法证明,当n=k+1时利用
是否仍然成立.有数学归纳法证明,当n=k+1时利用 转化为k项的形式.再通过构造即可得到结论.
转化为k项的形式.再通过构造即可得到结论.(1)∵
 ,
, ,故
,故 . 1分
. 1分令
 得
得 ;令
;令 得
得 . 3分
. 3分所以
 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 . 4分
. 4分(2)由
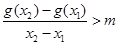
 变形得:
变形得: . 5分
. 5分令函数
 ,则
,则 在
在 上单调递增. 6分
上单调递增. 6分 即
即 在
在 上恒成立. 7分
上恒成立. 7分而
 (当且仅当
(当且仅当 时取“=”)
时取“=”)所以
 . 9分
. 9分(3)证明:不妨设
 ,由
,由
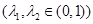 得:
得:





其中
 ,故上式的符号由因式“
,故上式的符号由因式“ ”的符号确定.
”的符号确定.令
 ,则函数
,则函数 .
. ,其中
,其中 ,得
,得 ,故
,故 .即
.即 在
在 上单调递减,且
上单调递减,且 .所以
.所以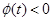 .
.从而有
 成立.
成立.该不等式能更进一步推广:
已知
 ,
, 是互不相等的实数,若正实数
是互不相等的实数,若正实数 满足
满足 ,则
,则
 .
.下面用数学归纳法加以证明:
i)当
 时,由(2)证明可知上述不等式成立;
时,由(2)证明可知上述不等式成立;ii)假设当
 时,上述不等式成立.即有:
时,上述不等式成立.即有: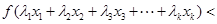
 .
.则当
 时,由
时,由 得:
得: ,于是有:
,于是有:
 .
.在该不等式的两边同时乘以正数
 可得:
可得:
 .
.在此不等式的两边同时加上
 又可得:
又可得:
 .
.该不等式的左边再利用i)的结论可得:

 .整理即得:
.整理即得:
 .
.所以,当
 时,上述不等式仍然成立.
时,上述不等式仍然成立.综上,对
 上述不等式都成立. 14分
上述不等式都成立. 14分
练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).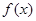 的解析式;
的解析式; 在
在 上有解,求实数
上有解,求实数 ,求
,求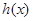 的单调区间.
的单调区间. (a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.
(a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________. ,则
,则 =________.
=________. +
+ +…+
+…+ =________.
=________. 的图象可能是( )
的图象可能是( )
 在区间
在区间 内的图象大致为( )
内的图象大致为( )