题目内容
在锐角△ABC中,已知内角A、B、C所对的边分别为a、b、c,且 (tanA-tanB)=1+tanA•tanB.
(tanA-tanB)=1+tanA•tanB.
(1)若a2-ab=c2-b2,求A、B、C的大小;
(2)已知向量 ,
, ,求
,求 |的取值范围.
|的取值范围.
解:因为 (tanA-tanB)=1+tanA•tanB,
(tanA-tanB)=1+tanA•tanB,
所以 ,
,
∴ .…(2分)
.…(2分)
(1)因为a2+b2-2abcosC=c2,所以cosC= ,∴
,∴ ,…(4分)
,…(4分)
 ,又
,又 ,
,
∴ ,
,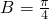 .…(6分)
.…(6分)
(2)因为向量 ,
, ,
,
∴ …(8分)
…(8分) .…(10分)
.…(10分)
 ,
, ,
,
 .…(12分)
.…(12分)
分析:利用 (tanA-tanB)=1+tanA•tanB求出A-B的值,
(tanA-tanB)=1+tanA•tanB求出A-B的值,
(1)通过余弦定理求出C的大小,得到A+B的值,即可求解A,B的值.
(2)直接求解模的平方,通过向量的数量积,利用两角和正弦函数公式化简表达式,结合A,B,C的范围,求出正弦函数的范围,然后 |的取值范围.
|的取值范围.
点评:本题是中档题,考查两角和正切、正弦函数以及向量的数量积、模的求法,考查计算能力,转化思想.
 (tanA-tanB)=1+tanA•tanB,
(tanA-tanB)=1+tanA•tanB,所以
 ,
,∴
 .…(2分)
.…(2分)(1)因为a2+b2-2abcosC=c2,所以cosC=
 ,∴
,∴ ,…(4分)
,…(4分) ,又
,又 ,
,∴
 ,
,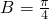 .…(6分)
.…(6分)(2)因为向量
 ,
, ,
,∴
 …(8分)
…(8分) .…(10分)
.…(10分) ,
, ,
, .…(12分)
.…(12分)分析:利用
 (tanA-tanB)=1+tanA•tanB求出A-B的值,
(tanA-tanB)=1+tanA•tanB求出A-B的值,(1)通过余弦定理求出C的大小,得到A+B的值,即可求解A,B的值.
(2)直接求解模的平方,通过向量的数量积,利用两角和正弦函数公式化简表达式,结合A,B,C的范围,求出正弦函数的范围,然后
 |的取值范围.
|的取值范围.点评:本题是中档题,考查两角和正切、正弦函数以及向量的数量积、模的求法,考查计算能力,转化思想.

练习册系列答案
相关题目