题目内容
(本小题满分16分)数列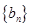
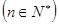 是递增的等比数列,且
是递增的等比数列,且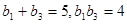 .
.
(1)求数列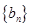 的通项公式;
的通项公式;
(2)若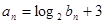 ,求证数列
,求证数列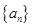 是等差数列;
是等差数列;
(3)若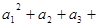 ……
……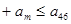 ,求
,求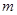 的最大值.
的最大值.
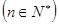 是递增的等比数列,且
是递增的等比数列,且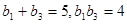 .
.(1)求数列
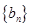 的通项公式;
的通项公式;(2)若
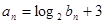 ,求证数列
,求证数列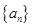 是等差数列;
是等差数列;(3)若
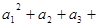 ……
……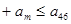 ,求
,求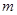 的最大值.
的最大值. (Ⅰ)等比数列{bn}的公比为 ,
,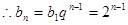 ;(Ⅱ)见解析;
;(Ⅱ)见解析;
(Ⅲ)最大值是7.
 ,
,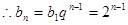 ;(Ⅱ)见解析;
;(Ⅱ)见解析;(Ⅲ)最大值是7.
试题分析: (1)根据韦达定理得到数列
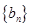 的首项和第三项,进而得到其通项公式。
的首项和第三项,进而得到其通项公式。(2)在第一问的基础上,可知得到数列an的通项公式,运用定义证明。
(3)根据数列的前n项和得到数列的和式,求解m的范围。
解:(Ⅰ)由
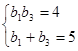 知
知 是方程
是方程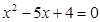 的两根,
的两根,注意到
 得
得 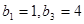 .……2分
.……2分 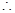
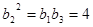 得
得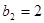 .
.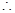

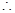 等比数列{bn}的公比为
等比数列{bn}的公比为 ,
,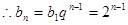 ……………………6分
……………………6分(Ⅱ)
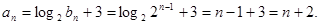 …………9分
…………9分∵

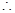 数列{an}是首项为3,公差为1的等差数列. …………………………11分
数列{an}是首项为3,公差为1的等差数列. …………………………11分(Ⅲ) 由(Ⅱ)知数列{an}是首项为3,公差为1的等差数列,有
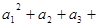 ……
……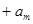 =
=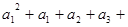 ……
……
=
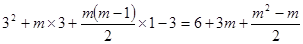 …………………………13分
…………………………13分∵
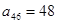
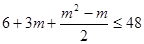 ,整理得
,整理得 ,
, 解得
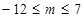 .
.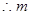 的最大值是7. …………16分.
的最大值是7. …………16分. 点评:解决该试题的关键是根据韦达定理来求解得到数列bn的首项与第三项的值。进而得到数列的an的通项公式。进而根据前n项和得到数列的求和。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
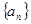 为等比数列,且首项为
为等比数列,且首项为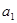 ,公比为
,公比为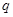 ,前
,前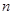 项和为
项和为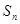 .
.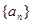 的首项
的首项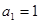 ,公比为
,公比为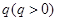 ,前
,前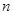 项和为
项和为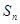 ,若
,若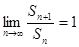 ,则公比
,则公比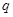 的取值范围是 .
的取值范围是 .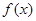 对应关系如表1所示,数列
对应关系如表1所示,数列 满足
满足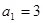 ,
, ,则
,则 .
.
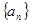 的各项均为正数,若
的各项均为正数,若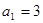 ,前三项的和为21 ,则
,前三项的和为21 ,则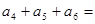 。
。 中,
中,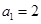 ,
,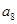 =4,函数
=4,函数 ,则
,则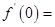 ( )
( )


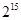
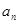 }的前n项和为
}的前n项和为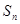 ,且
,且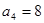 ,
, 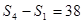 , 则数列{
, 则数列{ 满足:
满足: 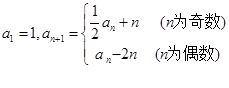
 ;
;  时,求
时,求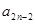 与
与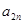 的关系式,并求数列
的关系式,并求数列