题目内容
设函数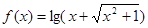
.
(1)确定函数f (x)的定义域；
(2)判断函数f (x)的奇偶性；
(3)证明函数f (x)在其定义域上是单调增函数；
(4)求函数f(x)的反函数.
【答案】
(1) R； (2) 奇函数；
(3)见解析； (4) 
【解析】解： (1)由
得x∈R，定义域为R. (2)是奇函数. (3)设x1，x2∈R，且x1＜x2，
则
. 令
，
则
.
=
=
=
∵x1－x2＜0，
，
，
，
∴t1－t2＜0，∴0＜t1＜t2，∴
，
∴f (x1)－f (x2)＜lg1=0，即f (x1)＜f (x2)，∴ 函数f(x)在R上是单调增函数.
(4)反函数为(x
R).
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
．
的极大值；
时，恒有
成立（其中
是函数
的导函数），试确定实数a的取值范围．
时，求y=T4（x）的解析式；
时（i∈N*，1≤i≤15），都有
恒成立．
.
，求函数
的极值；
，试确定
的单调性；
，且
在
上的最大值为M，证明：
．
.
，求函数
的极值；
，试确定
的单调性；
，且
在
上的最大值为M，证明：
．