题目内容
已知椭圆 过点
过点 ,且长轴长等于4.
,且长轴长等于4.
(1)求椭圆C的方程;
(2) 是椭圆C的两个焦点,圆O是以
是椭圆C的两个焦点,圆O是以 为直径的圆,直线
为直径的圆,直线 与圆O相切,并与椭圆C交于不同的两点A,B,若
与圆O相切,并与椭圆C交于不同的两点A,B,若 ,求
,求 的值.
的值.
(1) ,(2)
,(2)
【解析】
试题分析:(1)由题意,椭圆的长轴长 ,得
,得 ,
,
因为点 在椭圆上,所以
在椭圆上,所以 得
得 ,
,
所以椭圆的方程为 .
.
(2)由直线l与圆O相切,得 ,即
,即 ,
,
设 ,由
,由 消去y,整理得
消去y,整理得
由题意可知圆O在椭圆内,所以直线必与椭圆相交,所以 .
.

所以
因为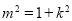 ,所以
,所以 .
.
又因为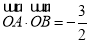 ,所以
,所以 ,
, ,得k的值为
,得k的值为 .
.
考点:本题考查椭圆的标准方程,直线与椭圆的位置关系

练习册系列答案
相关题目
 有公共渐近线的双曲线方程为( )
有公共渐近线的双曲线方程为( )



 的定义域为R,当
的定义域为R,当 时,
时, 是增函数,则
是增函数,则 的大小关系是
的大小关系是 >
> >
>
 >
> 若实数
若实数 满足
满足 则
则 ( )
( ) ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则该三棱锥外接球的表面积为____.
,则该三棱锥外接球的表面积为____. 值为3时,输出
值为3时,输出 的结果恰好是
的结果恰好是 ,则?处的关系式是( ).
,则?处的关系式是( ).
 B.
B. C.
C. D.
D.
 是
是 所在平面内一点,
所在平面内一点, ,现将一粒红豆随机撒在
,现将一粒红豆随机撒在 内,则红豆落在
内,则红豆落在 内的概率是
内的概率是  :
: 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,
上一点, 是直线
是直线 与
与 ,则
,则 = .
= .