题目内容
14.已知命题p:?x∈R,使得sinx=$\frac{3}{2}$;命题q:?x∈R,都有x2-x+1>0.则以下判断正确的是( )①命题“p∧q”是真命题;
②命题“p∧(¬q)”是假命题;
③命题“(¬p)∧q”是真命题;
④命题“p∨q”是假命题.
| A. | ②④ | B. | ②③ | C. | ③④ | D. | ①②③ |
分析 推导出命题p:?x∈R,使得sinx=$\frac{3}{2}$是假命题,命题q:?x∈R,都有x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0是真命题,由此利用复合命题的真假判断能求出结果.
解答 解:命题p:?x∈R,使得sinx=$\frac{3}{2}$是假命题,
命题q:?x∈R,都有x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0是真命题,
在①中,命题“p∧q”是假命题,故①错误;
在②中,命题“p∧(¬q)”是假命题,故②正确;
在③中,命题“(¬p)∧q”是真命题,故③正确;
在④中,命题“p∨q”是真命题,故④错误.
故选:B.
点评 本题考查考查命题真假的判断,考查复合命题真假判断、正弦函数、一元二次不等式等基础知识,考查推理论能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
19.若复数z满足z(1-i)2=|1-i|2,则z=( )
| A. | 1 | B. | -11 | C. | i | D. | -i |
3.把红、蓝、白3张纸牌随机地分发给甲、乙、丙三个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上都不对 |
11.设复数z满足3+i=z(2-i),则z=( )
| A. | 2-i | B. | 2+i | C. | 1-i | D. | 1+i |
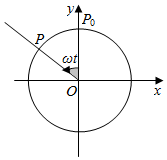 如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).
如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).