题目内容
(本小题满分12分)
设关于 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为 .
.
(1)当 时,求集合
时,求集合 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:解:(1)当 时,由已知得
时,由已知得 ,解得
,解得 ,所以
,所以
(2)由已知得
①若 时,因为
时,因为 ,所以
,所以 ,因为
,因为 ,所以
,所以 ,解得
,解得
②若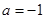 时,
时, ,显然有
,显然有 ,所以
,所以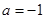 成立
成立
③若 时,因为
时,因为 ,所以
,所以 ,又
,又 ,
, ,
,
所以 ,解得
,解得 ,
,
综上所述,所求 的取值范围是
的取值范围是
考点:本试题考查了一元二次不等式的解法。
点评:解决该试题的关键是利用二次函数,二次方程与二次不等式来求解解集,同时能根据集合的包含关系来结合数轴法来表示参数的取值范围,注意端点值的取舍,这是个易错点,属于基础题。

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
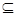 Q,求实数a的取值范围.
Q,求实数a的取值范围. ≤0},C={x||x-2|<4}.
≤0},C={x||x-2|<4}. ,若
,若 ,
, ,求实数
,求实数 、
、 的值。
的值。 ,
, ;若
;若 ,
, 。求|y1-y2|的最大值。
。求|y1-y2|的最大值。 ,
, ,
,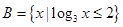 .
. ; (Ⅱ)求
; (Ⅱ)求 .
. 的定义域为A,函数
的定义域为A,函数 的值域为B。
的值域为B。 ,求
,求 .
. .若
.若 是
是 的充分而不必要条件,求正实数
的充分而不必要条件,求正实数 的取值范围。
的取值范围。 ,命题
,命题 :实数
:实数 为小于6的正整数,命题
为小于6的正整数,命题 :A是B成立的必要不充分条件.若命题
:A是B成立的必要不充分条件.若命题 是真命题,求实数
是真命题,求实数