题目内容
已知函数 ,且对于任意的x恒有f(x)≥f(x0),则x0=________.
,且对于任意的x恒有f(x)≥f(x0),则x0=________.
0
分析:由 ,知f′(x)=2x•2
,知f′(x)=2x•2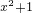 •ln2.令f′(x)=2x•2
•ln2.令f′(x)=2x•2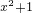 •ln2=0,得x=0.列表讨论知函数
•ln2=0,得x=0.列表讨论知函数 在x=0处取得最小值f(0)=2.由此能求出x0的值.
在x=0处取得最小值f(0)=2.由此能求出x0的值.
解答:∵ ,
,
∴f′(x)=2x•2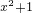 •ln2,
•ln2,
令f′(x)=2x•2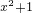 •ln2=0,得x=0.
•ln2=0,得x=0.
列表,讨论
∴函数 在x=0处取得极小值f(0)=2.
在x=0处取得极小值f(0)=2.
∵函数 只有一个极小值,故这个极小值就是函数
只有一个极小值,故这个极小值就是函数 的最小值.
的最小值.
∵函数 对于任意的x恒有f(x)≥f(x0),
对于任意的x恒有f(x)≥f(x0),
∴f(x)≥f(x)min=f(0),
∴x0=0.
故答案为:0.
点评:本题考查函数恒成立问题的应用,解题时要认真审题,仔细解答,注意导数性质的合理运用.
分析:由
 ,知f′(x)=2x•2
,知f′(x)=2x•2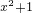 •ln2.令f′(x)=2x•2
•ln2.令f′(x)=2x•2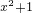 •ln2=0,得x=0.列表讨论知函数
•ln2=0,得x=0.列表讨论知函数 在x=0处取得最小值f(0)=2.由此能求出x0的值.
在x=0处取得最小值f(0)=2.由此能求出x0的值.解答:∵
 ,
,∴f′(x)=2x•2
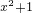 •ln2,
•ln2,令f′(x)=2x•2
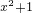 •ln2=0,得x=0.
•ln2=0,得x=0.列表,讨论
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
 在x=0处取得极小值f(0)=2.
在x=0处取得极小值f(0)=2.∵函数
 只有一个极小值,故这个极小值就是函数
只有一个极小值,故这个极小值就是函数 的最小值.
的最小值.∵函数
 对于任意的x恒有f(x)≥f(x0),
对于任意的x恒有f(x)≥f(x0),∴f(x)≥f(x)min=f(0),
∴x0=0.
故答案为:0.
点评:本题考查函数恒成立问题的应用,解题时要认真审题,仔细解答,注意导数性质的合理运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有 .
. 的解析式;
的解析式;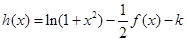 有几个零点?
有几个零点?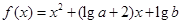 满足
满足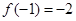 , 且对于任意
, 且对于任意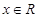 恒有
恒有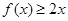 成立。
成立。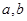 的值;
的值;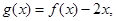 若存在实数
若存在实数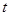 ,当
,当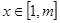 时,
时,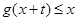 恒成立,求实数
恒成立,求实数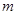 的最大值。
的最大值。 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有 .
. 的解析式;
的解析式; 在区间
在区间 上单调,求实数
上单调,求实数 的取值范围;
的取值范围; 有2个零点?求
有2个零点?求 的取值范围.
的取值范围.