题目内容
已知点P是曲线y=x2-ln x上的一个动点,则点P到直线l:y=x-2的距离的最小值为________.

[解析] 通解:设P(x,y),则点P到直线l的距离为
 令h(x)=x+ln x-x2-2,则h′(x)=1+
令h(x)=x+ln x-x2-2,则h′(x)=1+ -2x(x>0).令1+
-2x(x>0).令1+ -2x=0,解得x=1,即当0<x<1时,h′(x)>0,此时h(x)为增函数;当x>1时,h′(x)<0,此时h(x)为减函数.所以当x=1时,h(x)取最大值,h(x)max=1+ln 1-12-2=-2,所以|x+ln x-x2-2|min=2,所以点P到直线l的距离的最小值为
-2x=0,解得x=1,即当0<x<1时,h′(x)>0,此时h(x)为增函数;当x>1时,h′(x)<0,此时h(x)为减函数.所以当x=1时,h(x)取最大值,h(x)max=1+ln 1-12-2=-2,所以|x+ln x-x2-2|min=2,所以点P到直线l的距离的最小值为 =
= .
.
优解:y′=2x- (x>0),因为将直线l平移到与曲线第一次相切时,点P到直线l的距离最小,即为切点到直线l的距离,而直线l:y=x-2的斜率为1,所以令2x-
(x>0),因为将直线l平移到与曲线第一次相切时,点P到直线l的距离最小,即为切点到直线l的距离,而直线l:y=x-2的斜率为1,所以令2x- =1,解得x=1(x=-
=1,解得x=1(x=-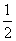 舍去),所以切点坐标为(1,1),它到直线y=x-2的距离为
舍去),所以切点坐标为(1,1),它到直线y=x-2的距离为 =
= ,即点P到直线l的距离的最小值为
,即点P到直线l的距离的最小值为 .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 B.
B.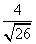
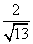 D.
D.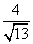

 B.
B. C.
C.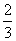 D.
D. },那么由函数y=f(x)的图象、x轴、直线x=
},那么由函数y=f(x)的图象、x轴、直线x=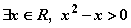 ”的否定是“对
”的否定是“对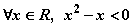 ” ;
” ;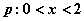 是
是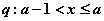 的必要不充分条件,则
的必要不充分条件,则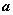 的取值范围是
的取值范围是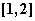 ;
;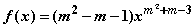 在
在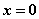 处有定义,则实数
处有定义,则实数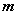 的值为2;
的值为2;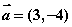 ,
,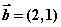 ,则向量
,则向量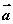 在向量
在向量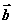 方向上的投影是
方向上的投影是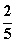 .
.