题目内容
已知中心在原点,焦点在坐标轴上的椭圆 ,它的离心率为
,它的离心率为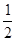 ,一个焦点和抛物线
,一个焦点和抛物线 的焦点重合,过直线
的焦点重合,过直线 上一点
上一点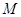 引椭圆
引椭圆 的两条切线,切点分别是
的两条切线,切点分别是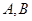 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若在椭圆 上的点
上的点 处的椭圆的切线方程是
处的椭圆的切线方程是 . 求证:直线
. 求证:直线 恒过定点
恒过定点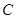 ;并出求定点
;并出求定点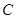 的坐标.
的坐标.
(Ⅲ)是否存在实数 ,使得
,使得 恒成立?(点
恒成立?(点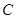 为直线
为直线 恒过的定点)若存在,求出
恒过的定点)若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(I)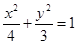 ;(II)直线AB恒过定点
;(II)直线AB恒过定点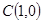 。
。
(III)存在实数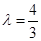 ,使得
,使得 。
。
解析试题分析:(I)设椭圆方程为 。抛物线
。抛物线 的焦点是
的焦点是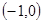 ,故
,故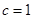 ,又
,又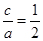 ,所以
,所以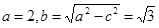 ,
,
所以所求的椭圆 方程为
方程为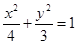 3分
3分
(II)设切点坐标为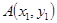 ,
,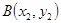 ,直线
,直线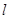 上一点M的坐标
上一点M的坐标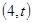 。
。
则切线方程分别为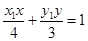 ,
,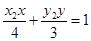 。
。
又两切线均过点M,即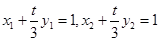 ,即点A,B的坐标都适合方程
,即点A,B的坐标都适合方程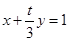 ,
,
而两点之间确定唯一的一条直线,故直线AB的方程是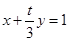 ,
,
显然对任意实数t,点(1,0)都适合这个方程,故直线AB恒过定点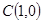 。 6分
。 6分
(III)将直线AB的方程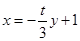 ,代入椭圆方程,得
,代入椭圆方程,得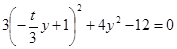 ,即
,即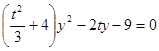
所以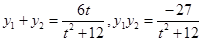 ..8分
..8分
不妨设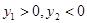
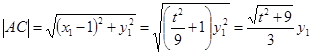 ,同理
,同理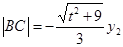 10分
10分
所以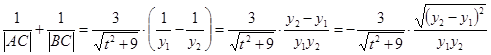
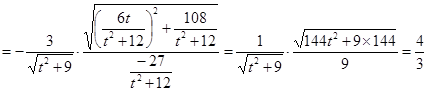
即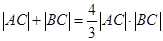 。
。
故存在实数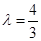 ,使得
,使得 。 12分
。 12分
考点:本题主要考查椭圆标准方程,直线方程,直线与椭圆的位置关系,存在性问题研究。
点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了椭圆的几何性质。对于存在性问题,往往先假设存在,利用已知条件加以探究,以明确计算的合理性。本题(III)通过假设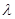 ,利用韦达定理进一步确定相等长度,求得了
,利用韦达定理进一步确定相等长度,求得了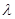 的值,达到证明目的。
的值,达到证明目的。

练习册系列答案
相关题目
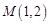 ,它们在
,它们在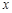 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.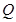 ,点
,点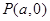 都满足
都满足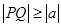 ,求
,求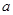 的取值范围.
的取值范围. 与椭圆
与椭圆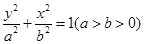 交于
交于 ,
, 两点,已知
两点,已知
 ,
,
 ,若
,若 且椭圆的离心率
且椭圆的离心率 ,又椭圆经过点
,又椭圆经过点 ,
, 为坐标原点.
为坐标原点. (
( 为半焦距),求直线
为半焦距),求直线 的值;
的值; 的中心在原点,焦点在
的中心在原点,焦点在 轴上,短轴的一个端点与左右焦点
轴上,短轴的一个端点与左右焦点 、
、 组成一个正三角形,焦点到椭圆上的点的最短距离为
组成一个正三角形,焦点到椭圆上的点的最短距离为 .
. 与椭圆
与椭圆 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围.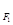 ,
,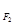 分别是椭圆E:
分别是椭圆E: +
+ =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过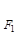 的直线
的直线 与E相交于A、B两点,且
与E相交于A、B两点,且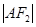 ,
,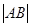 ,
, 成等差数列。
成等差数列。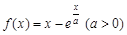 .
. 在
在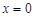 的切线能否与曲线
的切线能否与曲线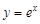 相切?并说明理由;
相切?并说明理由;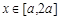 求
求 的最大值;
的最大值;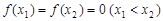 ,求证:
,求证: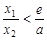 .
. ,
, 为直线
为直线 上任意一点,过
上任意一点,过 .
.
 三点的横坐标成等差数列;
三点的横坐标成等差数列; 时,
时, .求此时抛物线的方程。
.求此时抛物线的方程。 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F (1,0),离心率为
(1,0),离心率为 ,P为左顶点。
,P为左顶点。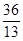 ,求直线AB的方程。
,求直线AB的方程。