题目内容
已知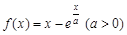 .
.
(Ⅰ)判断曲线 在
在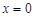 的切线能否与曲线
的切线能否与曲线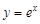 相切?并说明理由;
相切?并说明理由;
(Ⅱ)若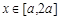 求
求 的最大值;
的最大值;
(Ⅲ)若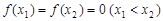 ,求证:
,求证: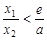 .
.
(1)曲线 在
在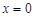 的切线不能与曲线
的切线不能与曲线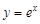 相切
相切
(2)当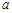 >
> ,即
,即 时,
时, .
.
当 ,即
,即 时,
时, =
=
 .
.
当 ,即
,即 时,
时,
(3)构造函数结合导数的知识里求解最值,证明不等式。
解析试题分析:解:(Ⅰ) ,则
,则 ,
, ,
,
∴曲线 在
在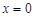 的切线l的方程为
的切线l的方程为 .
.
若l与曲线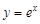 相切,设切点为
相切,设切点为 ,则
,则 .
.
由 ,得
,得 ,∴
,∴ ,得
,得 ,与
,与 矛盾.
矛盾.
∴曲线 在
在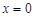 的切线不能与曲线
的切线不能与曲线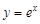 相切.
相切.
(Ⅱ),令 得
得 .
.
∴ .
.
∴ 在
在 上为增函数,在
上为增函数,在 上为减函数.
上为减函数.
∴当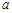 >
> ,即
,即 时,
时, .
.
当 ,即
,即 时,
时, =
=
 .
.
当 ,即
,即 时,
时, .
.
(Ⅲ)由(Ⅱ)知 =
=
 .
.
∵ ,∴
,∴ =
=

 .
.
∴ ,得
,得 ,∴
,∴ 且
且 .
.
得 ,又
,又 ,
,
∴ .
.
考点:导数的运用
点评:解决的关键是根据导数的符号判定函数的单调性,以及函数的最值,属于中档题。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 :
: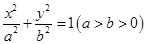 的一个焦点为
的一个焦点为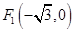 且过点
且过点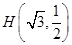 .
.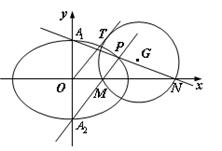
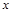 轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.
轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.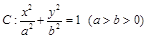 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,离心率为
,离心率为 , 在
, 在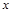 轴负半轴上有一点
轴负半轴上有一点 ,且
,且
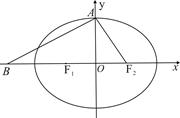
 三点的圆 恰好与直线
三点的圆 恰好与直线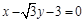 相切,求椭圆C的方程;
相切,求椭圆C的方程; 作斜率为
作斜率为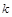 的直线
的直线 与椭圆C交于
与椭圆C交于 两点,在
两点,在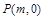 ,使得以
,使得以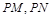 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由. ,它的离心率为
,它的离心率为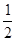 ,一个焦点和抛物线
,一个焦点和抛物线 的焦点重合,过直线
的焦点重合,过直线 上一点
上一点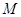 引椭圆
引椭圆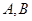 .
. 上的点
上的点 处的椭圆的切线方程是
处的椭圆的切线方程是 . 求证:直线
. 求证:直线 恒过定点
恒过定点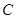 ;并出求定点
;并出求定点 ,使得
,使得 恒成立?(点
恒成立?(点 的离心率
的离心率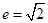 且点
且点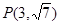 在双曲线C上.
在双曲线C上.  求直线l的方程.
求直线l的方程. 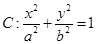
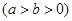 的离心率为
的离心率为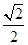 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线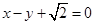 相切.
相切.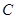 的方程;
的方程;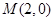 的直线与椭圆
的直线与椭圆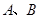 ,设
,设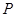 为椭圆上一点,且满足
为椭圆上一点,且满足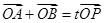 (其中
(其中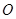 为坐标原点),求整数
为坐标原点),求整数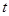 的最大值.
的最大值. (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 的椭圆
的椭圆 与抛物线
与抛物线 在
在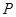 .
.
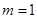 时,求椭圆的方程;
时,求椭圆的方程; 经过椭圆
经过椭圆 、
、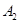 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数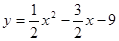 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
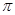 )。
)。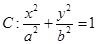 的左焦点
的左焦点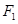 的坐标为
的坐标为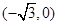 ,
,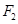 是它的右焦点,点
是它的右焦点,点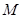 是椭圆
是椭圆 上一点,
上一点, 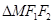 的周长等于
的周长等于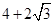 .
.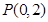 作直线
作直线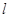 与椭圆
与椭圆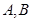 ,且
,且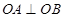 (其中
(其中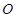 为坐标原点),求直线
为坐标原点),求直线