题目内容
命题“
”的否定是_ ；
解析试题分析：题目中所给的命题是全称命题，全称命题的否定是特称命题.
考点：本小题主要考查全程命题的否定.
点评：解决含有量词的否定的问题时，要注意全称命题的否定是特称命题，特称命题的否定是全称命题.
练习册系列答案
相关题目
给出下列四个命题：
（1）命题“若
，则
”的逆否命题为假命题；
（2）命题
．则
，使
；
（3）“
”是“函数
为偶函数”的充要条件；
（4）命题
“
，使
”；命题
“若
，则
”，那么
为真命题．其中正确的个数是（ ）
A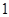． | B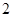． | C． | D． |
已知条件
条件,
直线
与圆
相切，则
是
的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
给出三个命题：
①若两条直线和第三条直线所成的角相等，则这两条直线互相平行；
②若两条直线都与第三条直线垂直，则这两条直线互相平行；
③若两条直线都与第三条直线平行，则这两条直线互相平行。其中真命题个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
设
则“
且
”是“
”的
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．即不充分也不必要条件 |
设p、q是两上命题，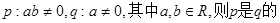
（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
“
”是“
”的 ( )
| A．必要不充分条件 | B．充分不必要条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知
表示两个不同的平面，
是一条直线，且
，则“
”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
已知
：函数
与
轴有两个交点；
：
，
恒成立．若
为真，则实数m的取值范围为 ( )
A． | B． |
C． | D． |