Question

给出下列四个命题：
（1）命题“若，则”的逆否命题为假命题；
（2）命题．则，使；
（3）“”是“函数为偶函数”的充要条件；
（4）命题“，使”；命题“若，则”，那么为真命题．其中正确的个数是（　　）

A．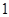

B．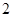

C．

D．

Answer 1

B

解析试题分析：（1）因为原命题为真，所以逆否命题也为真。所以命题“若，则”的逆否命题为假命题；，错误；
（2）因为全称命题的否定为特称命题，所以命题．则，使，正确；
（3）“”是“函数为偶函数”的充要条件，正确。
（4）命题“，使”，错误；命题“若，则”，错误，那么为真命题，是错误的。
考点：四种命题及四种命题间的关系；全称命题的否定；三角函数的奇偶性；复合命题真假的判断。
点评：（1）若函数y=Asin（ωx+φ）为偶函数，则；若函数y=Asin（ωx+φ）为奇函数，则。（2）熟练掌握全称命题的否定方法“?x∈A，非p（x）”的否定是“?x∈A，p（x）”。