题目内容
如果一个几何体的三视图如图（单位长度：cm），则此几何体的体积是（ ）分析：由三视图画出几何体的直观图，判断几何体的高与底面边长，代入公式计算即可．
解答：解：由三视图判断几何体为正四棱锥与正四棱柱的组合体，如图：
正四棱锥的底面边长为4，高为2，∴V四棱锥=
×4×4×2=
；
正四棱柱的底面边长为4，高为4，∴V四棱柱=4×4×4=64；
∴几何体的体积是
，
故选A．
正四棱锥的底面边长为4，高为2，∴V四棱锥=
| 1 |
| 3 |
| 32 |
| 3 |
正四棱柱的底面边长为4，高为4，∴V四棱柱=4×4×4=64；
∴几何体的体积是
| 224 |
| 3 |
故选A．
点评：本题考查由三视图求几何体的面积、体积．关键是判断几何体的形状与有关数据．
练习册系列答案
相关题目
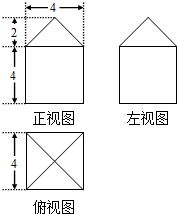如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（ ）| A、96cm3 | ||
| B、80cm3 | ||
C、（80+16
| ||
D、
|
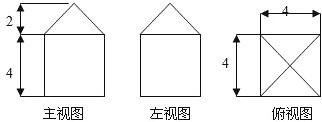
如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是
如果一个几何体的三视图如图所示，则此几何体的体积是（ ）