题目内容
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且该椭圆过定点
,且该椭圆过定点 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,求对角线
,求对角线![]() 长度的最小值.
长度的最小值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
试题分析:(1)要求椭圆标准方程,实质就是要求![]() 的值,就是找两个关于
的值,就是找两个关于![]() 的等量关系,本题中焦点已知说明
的等量关系,本题中焦点已知说明![]() ,又有椭圆过点
,又有椭圆过点![]() ,只要把点
,只要把点![]() 的坐标代入可得
的坐标代入可得![]() 的一个等式,两者结合可解得
的一个等式,两者结合可解得![]() ;(2)此时中直线
;(2)此时中直线![]() 的斜率可以不存在,但一定不会为0,为了避免分类可设直线
的斜率可以不存在,但一定不会为0,为了避免分类可设直线![]() 方程为
方程为![]() ,下面我们只要把
,下面我们只要把![]() 的长表示为
的长表示为![]() 的函数,设
的函数,设![]() ,把
,把![]() 代入椭圆方程化简后可得
代入椭圆方程化简后可得![]() ,由
,由![]() 可得
可得![]() ,因此
,因此![]() ,这样可由
,这样可由![]() 得
得![]() ,而
,而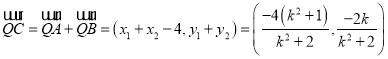 ,因此
,因此![]() 可用
可用![]() 表示出来,由函数和性质可得其最小值.
表示出来,由函数和性质可得其最小值.
试题解析:(1)![]() ,标准方程为
,标准方程为![]() .
.
(2)设直线![]() ,由
,由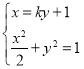 ,得
,得![]() ,
,
设![]() ,则
,则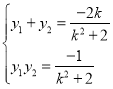 得
得![]()
从而![]()
由![]() 得
得![]() ,从而
,从而![]() ,解得
,解得![]()
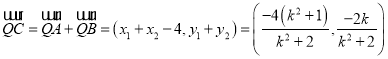 ,
,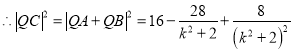 ,令
,令![]() ,则
,则![]() ,
,![]() 当
当![]() 时,
时,![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】全国人民代表大会在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作.调查发现,男、女记者中分别有10人和6人会俄语.
(1)根据以上数据完成以下![]() 列联表:
列联表:
会俄语 | 不会俄语 | 总计 | |
男 | |||
女 | |||
总计 |
(2)能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”