题目内容
已知f(x)=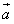
·
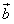-1，其中向量
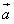=（sin2x，2cosx），
=（
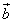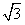，cosx），(x∈R)。
（1）求f(x)的最小正周期和最小值；
（2）在△ABC中，角A、B、C的对边分别为a、b、c，若f(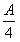
)=
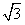，a=2
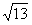，b=8，求边长c的值。
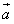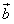·-1，其中向量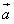=（sin2x，2cosx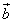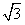），=（，cosx），(x∈R)。（1）求f(x)的最小正周期和最小值；
（2）在△ABC中，角A、B、C的对边分别为a、b、c，若f(
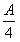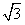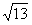)=，a=2，b=8，求边长c的值。 解：（1）f(x)=a·b-1=(sin2x，2cosx)·(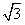
，cosx)-1
=
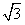sin2x+2cos2x-1=
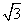sin2x+cos2x=2sin（2x+
），
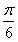∴f(x)的最小正周期为π，最小值为-2。
（2）
，
∴
，∴
，
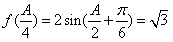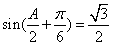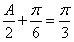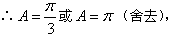
由余弦定理，得a2=b2+c2-2bccosA，
52=64+c2-8c，即c2-8c+12=0，从而c=2或c=6。
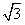，cosx)-1=
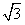sin2x+2cos2x-1=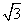sin2x+cos2x=2sin（2x+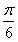），∴f(x)的最小正周期为π，最小值为-2。
（2）
，∴
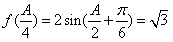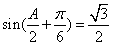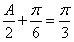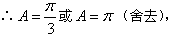
，∴，由余弦定理，得a2=b2+c2-2bccosA，
52=64+c2-8c，即c2-8c+12=0，从而c=2或c=6。
练习册系列答案
字词句段篇系列答案
相关题目