题目内容
已知函数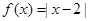
(1)解不等式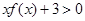 ;
;
(2)对于任意的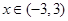 ,不等式
,不等式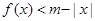 恒成立,求
恒成立,求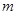 的取值范围.
的取值范围.
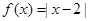
(1)解不等式
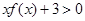 ;
;(2)对于任意的
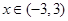 ,不等式
,不等式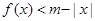 恒成立,求
恒成立,求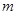 的取值范围.
的取值范围.(1)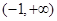 ;(2)
;(2)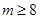 .
.
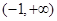 ;(2)
;(2)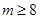 .
.试题分析:本题考查绝对值不等式的解法和不等式的恒成立问题,考查学生的分类讨论思想和转化能力.第一问,利用零点分段法进行分类求解;第二问,利用函数的单调性求出最大值证明恒成立问题.
试题解析:(1)
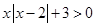
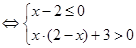 或
或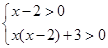 3分
3分解得
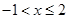 或
或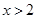 ∴不等式解集为
∴不等式解集为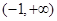 6分
6分(2)
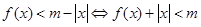 ,即
,即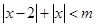 , 7分
, 7分设
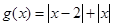
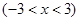 ,则
,则 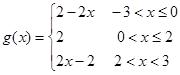 9分
9分  在
在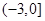 上单调递减,
上单调递减,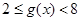 ;
;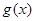 在
在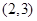 上单调递增,
上单调递增,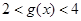
∴在
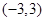 上
上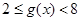 , 11分
, 11分故
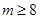 时不等式
时不等式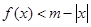 在
在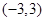 上恒成立 12分
上恒成立 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
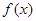 的定义域为
的定义域为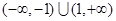 ,对定义域内的任意x,满足
,对定义域内的任意x,满足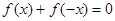 ,当
,当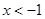 时,
时,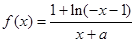 (a为常),且
(a为常),且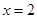 是函数
是函数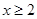 时,不等式
时,不等式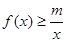 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;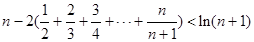
 小时的收费为
小时的收费为 元
元 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动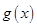 元
元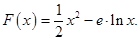
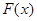 的极值;
的极值;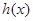 和
和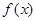 定义域内的任意实数
定义域内的任意实数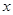 ,若存在常数
,若存在常数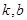 ,使得不等式
,使得不等式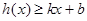 和
和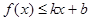 都成立,则称直线
都成立,则称直线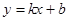 是函数
是函数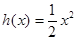 ,
,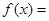
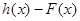 ,试问函数
,试问函数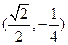 ,则a=
,则a=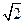
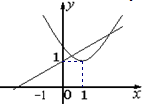
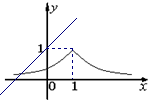

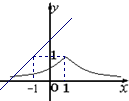
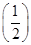 x是R上的1高调函数;
x是R上的1高调函数;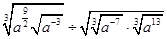 ;
;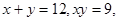 且
且 ,求
,求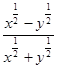 的值.
的值. 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.
 ,求用
,求用 表示
表示 的函数关系式;
的函数关系式;