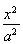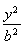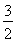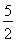Question

双曲线=1(a＞1,b＞0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1，0)到直线l的距离与点(-1，0)到直线l的距离之和s≥c.求双曲线的离心率e的取值范围.

Answer 1

解：直线l的方程为=1,即bx+ay-ab=0.

由点到直线的距离公式，且a＞1,得到点(1，0)到直线l的距离d₁=.

同理得到点(-1，0)到直线l的距离：

d₂=,s=d₁+d₂=.

由s≥c,得

即5a≥2c².于是得5≥2e²,

即4e⁴-25e²+25≤0.

解不等式，得≤e²≤5.

由于e＞1＞0,

所以e的取值范围是≤e≤.

温馨提示

本题通过构造法来求离心率的取值范围，考查了不等式的数学思想，点到直线的距离公式，双曲线的基本性质，以及综合运算能力.