题目内容
已知F1、F2是双曲线A.![]() B.
B.![]() +1 C.
+1 C.![]() -1 D.
-1 D.![]() +1
+1
解析:由对称性知△F1F2P为等腰Rt△,
∴|F1F2|=|PF1|.
将x=-c代入双曲线方程可求得|yP|=![]() .
.
∴2c=![]() 4a2c2=b4
4a2c2=b4![]() 4a2c2=(c2-a2)2
4a2c2=(c2-a2)2![]() 4e2=(e2-1)2
4e2=(e2-1)2![]() e2=3±2
e2=3±2![]() .
.
∵e>1,∴取e2=3+2![]() =(
=(![]() +1)2.
+1)2.
∴e=![]() +1.
+1.
答案:B

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
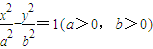 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若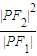 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )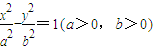 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若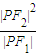 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )