题目内容
16.已知集合A={(x,y)|y=x2+mx+2},B={(x,y)|y=x+1},如果A∩B≠∅,则实数m的取值范围为{m|m≥3或m≤-1}.分析 联立方程组$\left\{\begin{array}{l}{y={x}^{2}+mx+2}\\{y=x+1}\end{array}\right.$,得x2+(m-1)x+1=0,由A∩B≠∅,将题目中的问题转化为方程x2+(m-1)x+1=0在R内有解.由此能求出实数m的取值范围.
解答 解:∵集合A={(x,y)|y=x2+mx+2},B={(x,y)|y=x+1},
∴联立方程组$\left\{\begin{array}{l}{y={x}^{2}+mx+2}\\{y=x+1}\end{array}\right.$,
消去y得x2+(m-1)x+1=0,
∵A∩B≠∅,
∴将题目中的问题转化为方程x2+(m-1)x+1=0在R内有解.
∴△=(m-1)2-4≥0,
解得m≥3或m≤-1,
∴实数m的取值范围为:{m|m≥3或m≤-1}.
故答案为:{m|m≥3或m≤-1}.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
6.函数f(x)=x3+sinx+2(x∈R),若f(a)=2,则f(-a)的值为( )
| A. | 5 | B. | -2 | C. | 1 | D. | 2 |
4.下列函数中,是偶函数且不存在零点的是( )
| A. | y=x2 | B. | y=$\sqrt{x}$ | C. | y=log2x | D. | y=($\frac{1}{2}$)|x| |
11.设a、b分别是甲、乙各抛掷一枚骰子得到的点数,已知乙所得的点数为2,则方程x2+ax+b=0有两个不相等的实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
1.抛物线y=6x2的焦点坐标为( )
| A. | (0,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,0) | C. | (0,$\frac{1}{24}$) | D. | ($\frac{1}{24}$,0) |
8.椭圆上$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点p到两焦点距离之积为m,则m取最大值时,p点的坐标是( )
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
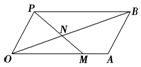 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.