题目内容
椭圆的中心是原点O,它的短轴长为(1)求椭圆的方程;
(2)若![]() ·
·![]() =0,求直线PQ的方程;
=0,求直线PQ的方程;
(3)设![]() (λ>1),过点P且平行于准线l的直线与椭圆相交于另一点M,求证:
(λ>1),过点P且平行于准线l的直线与椭圆相交于另一点M,求证:![]() .
.
答案:(1)解:由题意,可设椭圆的方程为![]() =1(a>
=1(a>![]() ).由已知得
).由已知得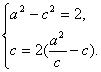
解得a=![]() ,c=2,所以椭圆的方程为
,c=2,所以椭圆的方程为![]() =1.
=1.
(2)解:由(1)可得A(3,0).设直线PQ的方程为y=k(x-3).由方程组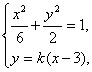
得(3k2+1)x2-18k2x+27k2-6=0,
依题意Δ=12(2-3k2)>0,得![]() <k<
<k<![]() .
.
设P(x1,y1),Q(x2,y2),则x1+x2=![]() , ①
, ①
x1x2=![]() . ②
. ②
于是y1y2=k2(x1-3)(x2-3)=k2[x1x2-3(x1+x2)+9]. ③
∵![]() =0,∴x1x2+y1y2=0. ④
=0,∴x1x2+y1y2=0. ④
由①②③④得5k2=1,从而k=±![]() ∈(
∈(![]() ).
).
所以直线PQ的方程为x![]() y-3=0或x+
y-3=0或x+![]() y-3=0.
y-3=0.
(3)证明:![]() =(x1-3,y1),
=(x1-3,y1),![]() =(x2-3,y2).
=(x2-3,y2).
由已知得方程组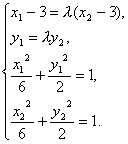 注意λ>1,解得x2=
注意λ>1,解得x2=![]() ,
,
因F(2,0),M(x1,-y1),故![]() =(x1-2,-y1)=(λ(x2-3)+1,-y1)=(
=(x1-2,-y1)=(λ(x2-3)+1,-y1)=(![]() ,-y1)=-λ(
,-y1)=-λ(![]() ,y2).
,y2).
而![]() =(x2-2,y2)=(
=(x2-2,y2)=(![]() ,y2),所以
,y2),所以![]() =-λ
=-λ![]() .
.

 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)( )的准线
)的准线 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 . ,求直线PQ的方程;
,求直线PQ的方程; (
( ),过点P且平行于准线
),过点P且平行于准线 .
.