题目内容
椭圆的中心是原点O,它的短轴长为 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)( )的准线
)的准线 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
(1)求椭圆的方程及离心率;
(2)若 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设 (
( ),过点P且平行于准线
),过点P且平行于准线 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明 .
.
【答案】
(1)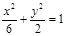 ,离心率
,离心率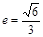 .(2)
.(2)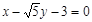 或
或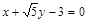 .(3)证明:见解析。
.(3)证明:见解析。
【解析】
试题分析:(1)由题意,可设椭圆的方程为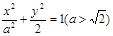 .由已知得
.由已知得
解得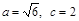 ,所以椭圆的方程为
,所以椭圆的方程为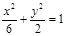 ,离心率
,离心率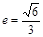 .
.
(2)解:由(1)可得A(3,0) .设直线PQ的方程为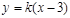 .由方程组
.由方程组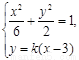
得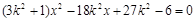 ,依题意
,依题意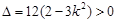 ,得
,得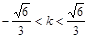 .
.
设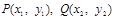 ,则
,则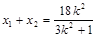 ,
①
,
①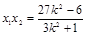 . ②,由直线PQ的方程得
. ②,由直线PQ的方程得
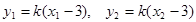 .于是
.于是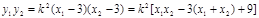 .
③
.
③
∵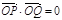 ,∴
,∴ .
④,由①②③④得
.
④,由①②③④得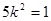 ,从而
,从而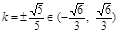 .
.
所以直线PQ的方程为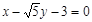 或
或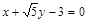 .
.
(3)证明: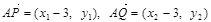 .由已知得方程组
.由已知得方程组
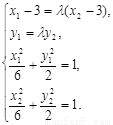 注意
注意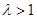 ,解得
,解得 ,因
,因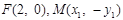 ,故
,故
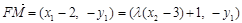
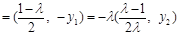 .
.
而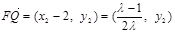 ,所以
,所以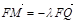 .
.
考点:本题主要考查椭圆的标准方程、直线与椭圆的位置关系以及平面向量的基础知识。
点评:是一道综合性较强的题目,较全面的考查了椭圆、直线于椭圆以及平面向量的基础知识。解答中从联立方程组出发,运用韦达定理,体现了整体观,是解析几何问题中的常见类型。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目