题目内容
已知 .
.
(1) 若 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;
(2) 若 ,求证:当
,求证:当 时,
时, 恒成立;
恒成立;
(3) 利用(2)的结论证明:若 ,则
,则 。
。
解:(1)当 时,
时,
∴ .
.
∵  有单调减区间,∴
有单调减区间,∴ 有解,即
有解,即
∵  ,∴
,∴  有解。
有解。
(ⅰ)当 时符合题意;
时符合题意;
(ⅱ)当 时,△
时,△ ,即
,即 。
。
∴ 的取值范围是
的取值范围是 。
。
(2)当 时,设
时,设 ,
,
∴  。
。
∵ ,
,
讨论 的正负得下表:
的正负得下表:
 …
…
∴当 时
时 有最大值0.
有最大值0.
即 恒成立。
恒成立。
∴当 时,
时, 恒成立。
恒成立。
(3)∵ ,
,
∴



由(2)有
∴

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 是曲线
是曲线 的切线,则实数
的切线,则实数 的值为 .
的值为 .  的一条切线
的一条切线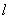 与直线
与直线 垂直,则
垂直,则 B.
B.  C.
C. D.
D. 
 .的部分图象如图所示,其中点P是图象的一个最高点。
.的部分图象如图所示,其中点P是图象的一个最高点。 的解析式;
的解析式; 且
且 ,求
,求 .
.
 ,抛物线
,抛物线 的焦点是
的焦点是 ,若抛物线上存在一点
,若抛物线上存在一点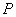 ,使得
,使得 最小,则
最小,则 (B)
(B) (C)
(C) (D)
(D)
 的图象为
的图象为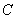 ,有如下结论:①图象
,有如下结论:①图象 对称;②图象
对称;②图象 对称;③函数
对称;③函数 在区间
在区间 内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号)
内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号) 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线 和直线
和直线 的距离之和的最小值( )
的距离之和的最小值( ) D.
D.
 、
、 ,则下列判断正确的是( )
,则下列判断正确的是( ) 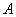 .
. ,甲比乙成绩稳定
,甲比乙成绩稳定 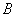 .
.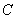 .
. ,甲比乙成绩稳定
,甲比乙成绩稳定 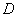 .
.