题目内容
过椭圆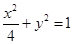 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于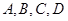 四点,则四边形
四点,则四边形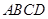 面积的最大值与最小值之差为( )
面积的最大值与最小值之差为( )
(A)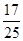 (B)
(B)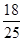 (C)
(C)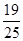 (D)
(D)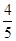
【答案】
B
【解析】
试题分析:当 为
为 ,
, 轴时,此时
轴时,此时 (通径),面积取最大值为
(通径),面积取最大值为 ;当两条直线斜率都存在时,设直线
;当两条直线斜率都存在时,设直线 的方程为
的方程为 ,与椭圆
,与椭圆 联立后得:
联立后得: ,设
,设 ,则
,则
 ,
, ,
,
同理 ,所以
,所以 ,
,
因为 ,所以
,所以 ,因而
,因而 ,故选B.
,故选B.
考点:1.椭圆中方程的联立问题;2.弦长公式以及四边形面积公式.

练习册系列答案
相关题目
过椭圆
+y2=1的左焦点作互相垂直的两条直线,分别交椭圆于A、B、C、D四点,则四边形ABCD面积的最大值与最小值之差为( )
| x2 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过椭圆
+y2=1的左焦点作互相垂直的两条直线,分别交椭圆于A、B、C、D四点,则四边形ABCD面积的最小值为( )
| x2 |
| 4 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
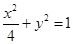 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于 四点,则四边形
四点,则四边形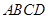 面积的最小值为( )
面积的最小值为( )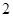 (B)
(B) 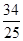 (C)
(C) 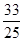 (D)
(D)
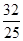
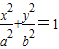 的左、右焦点F1、F2所作的两条互相垂直的直线l1、l2的交点在此椭圆的内部,则此椭圆的离心率的取值范围是 .
的左、右焦点F1、F2所作的两条互相垂直的直线l1、l2的交点在此椭圆的内部,则此椭圆的离心率的取值范围是 .