题目内容
 (2010•广东模拟)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
(2010•广东模拟)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.(1)求四棱锥P-ABCD的体积V;(2)求证:PB⊥DM;(3)求截面ADMN的面积.
分析:(1)由已知中PA=AD=AB=2BC=2,可求出底面ABCD的面积,由PA垂直于底面ABCD,可得PA即为棱锥的高,代入棱锥体积公式,可得答案.
(2)由PA=AB,N为PB中点,可得AN⊥PB,由A点三棱相互垂直,可得AD⊥平面PAB,进而AD⊥PB,结合线面垂直的判定定理可得PB⊥平面ANMD,进而得到PB⊥DM;
(3)由已知及(2)中结论,可得截面ADMN为直角梯形,求出上下底及高,代入梯形面积公式,可得答案.
(2)由PA=AB,N为PB中点,可得AN⊥PB,由A点三棱相互垂直,可得AD⊥平面PAB,进而AD⊥PB,结合线面垂直的判定定理可得PB⊥平面ANMD,进而得到PB⊥DM;
(3)由已知及(2)中结论,可得截面ADMN为直角梯形,求出上下底及高,代入梯形面积公式,可得答案.
解答: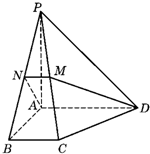 (1)解:由AD=AB=2BC=2,得底面直角梯形ABCD的面积
(1)解:由AD=AB=2BC=2,得底面直角梯形ABCD的面积
S=
×AB=3,
由PA⊥底面ABCD,得四棱锥P-ABCD的高h=PA=2,
所以四棱锥P-ABCD的体积V=
Sh=
×3×2=2. …(4分)
(2)证明:因为N是PB的中点,PA=PB,所以AN⊥PB. …(5分)
由PA⊥底面ABCD,得PA⊥AD,…(6分)
又∠BAD=90°,即BA⊥AD,
∴AD⊥平面PAB,所以AD⊥PB,…(8分)
∴PB⊥平面ADMN,
∴PB⊥DM. …(10分)
(3)由M,N分别为PC,PB的中点,得MN∥BC,且MN=
BC=
,
又AD∥BC,故MN∥AD,
由(2)得AD⊥平面PAB,又AN?平面PAB,故AD⊥AN,
∴四边形ADMN是直角梯形,
在Rt△PAB中,PB=
=2
,
AN=
PB=
,
∴截面ADMN的面积S=
(MN+AD)×AN=
. …(14分)
 (1)解:由AD=AB=2BC=2,得底面直角梯形ABCD的面积
(1)解:由AD=AB=2BC=2,得底面直角梯形ABCD的面积S=
| BC+AD |
| 2 |
由PA⊥底面ABCD,得四棱锥P-ABCD的高h=PA=2,
所以四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
(2)证明:因为N是PB的中点,PA=PB,所以AN⊥PB. …(5分)
由PA⊥底面ABCD,得PA⊥AD,…(6分)
又∠BAD=90°,即BA⊥AD,
∴AD⊥平面PAB,所以AD⊥PB,…(8分)
∴PB⊥平面ADMN,
∴PB⊥DM. …(10分)
(3)由M,N分别为PC,PB的中点,得MN∥BC,且MN=
| 1 |
| 2 |
| 1 |
| 2 |
又AD∥BC,故MN∥AD,
由(2)得AD⊥平面PAB,又AN?平面PAB,故AD⊥AN,
∴四边形ADMN是直角梯形,
在Rt△PAB中,PB=
| PA2+AB2 |
| 2 |
AN=
| 1 |
| 2 |
| 2 |
∴截面ADMN的面积S=
| 1 |
| 2 |
5
| ||
| 4 |
点评:本题考查的知识点是空间中直线与直线之间的位置关系,棱锥的体积,(1)的关键是计算出棱锥的底面面积及高,(2)的关键是证明 得PB⊥平面ANMD,(3)的关键是判断出截面的形状.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目